
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để M là số nguyên
Thì (x2–5) chia hết cho (x2–2)
==>(x2–2–3) chia hết cho (x2–2)
==>[(x2–2)—3] chia hết cho (x2–2)
Vì (x2–2) chia hết cho (x2–2)
Nên 3 chia hết cho (x2–2)
==> (x2–2)€ Ư(3)
==> (x2–2) €{1;-1;3;-3}
TH1: x2–2=1
x2=1+2
x2=3
==> ko tìm được giá trị của x
TH2: x2–2=-1
x2=-1+2
x2=1
12=1
==>x=1
TH3: x2–2=3
x2=3+2
x2=5
==> không tìm được giá trị của x
TH4: x2–2=-3
x2=-3+2
x2=-1
(-1)2=1
==> x=-1
Vậy x € {1;—1)

a: \(=\dfrac{1}{4}\cdot4-\dfrac{3}{4}\cdot\dfrac{4}{5}=1-\dfrac{3}{5}=\dfrac{2}{5}\)

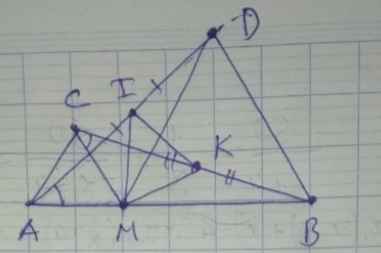
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M

Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

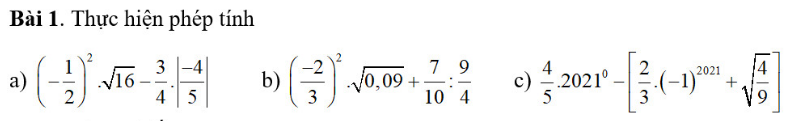




Chẳng thấy rõ chữ
Bạn bấm đọc tiếp nha