
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có: \(\left(x-2\right)^{2018}+\left|y^2-9\right|^{2017}=0\)
Suy ra: \(\hept{\begin{cases}\left(x-2\right)^{2018}=0\\\left|y^2-9\right|^{2017}=0\end{cases}}\)
<=> \(\hept{\begin{cases}x-2=0\\\left|y^2-9=0\right|\end{cases}}\)
<=> \(\hept{\begin{cases}x=2\\y=\orbr{\begin{cases}3\\-3\end{cases}}\end{cases}}\)\(\hept{\begin{cases}x=2\\y=\orbr{\begin{cases}3\\-3\end{cases}}\end{cases}}\)
chưa chắc đã đúng đâu Nguyệt Phượng nhé
trường hợp của bạn chỉ dùng khi biểu thức trên là:(x-2)^2018* |y^2-9|^ 2017=0 thôi bạn nhé

Ta có \(\frac{x-3}{x+5}=\frac{5}{7}\)
=> 5( x + 5 ) = 7( x - 3 )
=> 5x + 25 = 7x - 21
=> 7x - 5x = 25 + 21
=> 2x = 46
=> x = 23

a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{2021a}{2021b}=\dfrac{2021a-c}{2021b-d}\)
c, Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2\)
Áp dụng t/c dtsbn:
\(\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2=\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\)

\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)

a) (-4,3)+\(\left[\left(-7,5\right)+4,3\right]\)
=\(\left(-4,3\right)+4,3+\left(-7,5\right)\)
=-7,5
b)\(45,3+\left[-7,3+\left(-22\right)\right]\)
=\(45,3-7,3+\left(-22\right)\)
=38-22
=16
c)\(\left[\left(-11,7\right)+5,5\right]+\left[11,7+\left(-2,5\right)\right]\)
=\(\left[\left(-11,7\right)+11,7\right]+5,5-2,5\)
=\(3\)



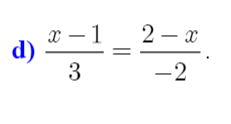
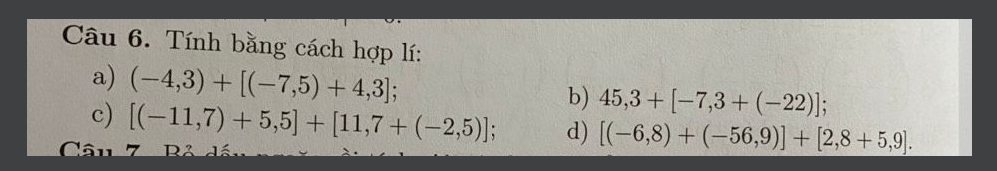
B
B
Thanks