
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cái đấy ko thuộc trong chương trình lớp 7 đâu bạn!!Phải các anh chị lớp 8,9 mới giải đc!!!!!

a. Xét tam giác ABD và tam giác HBD có:
góc BAD = góc BHD = 90 độ
BD là cạnh chung
góc ABD = góc HBD ( BD là tia phân giác của góc B)
Vậy tam giác ABD = tam giác HBD ( cạnh huyền - góc nhọn)


1: \(75^3:\left(-25\right)^3=\left(\dfrac{75}{-25}\right)^3=\left(-3\right)^3=-27\)
2: \(\left(-60\right)^2:\left(-5\right)^2=\dfrac{60^2}{5^2}=12^2=144\)
3: \(169^2:\left(-13\right)^2=\dfrac{169^2}{13^2}=\left(\dfrac{169}{13}\right)^2=13^2=169\)
4: \(\left(\dfrac{1}{2}\right)^2:\left(\dfrac{3}{2}\right)^2=\left(\dfrac{1}{2}:\dfrac{3}{2}\right)^2=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)
5: \(\left(\dfrac{2}{3}\right)^3:\left(\dfrac{8}{27}\right)^3=\left(\dfrac{2}{3}:\dfrac{8}{27}\right)^3=\left(\dfrac{2}{3}\cdot\dfrac{27}{8}\right)^3=\left(\dfrac{9}{4}\right)^3=\dfrac{729}{64}\)
6: \(\left(\dfrac{5}{4}\right)^4:\left(\dfrac{15}{2}\right)^4=\left(\dfrac{5}{4}:\dfrac{15}{2}\right)^4=\left(\dfrac{5}{4}\cdot\dfrac{2}{15}\right)^4=\left(\dfrac{1}{6}\right)^4=\dfrac{1}{1296}\)
7: \(\left(\dfrac{7}{8}\right)^5:\left(\dfrac{21}{16}\right)^5\)
\(=\left(\dfrac{7}{8}:\dfrac{21}{16}\right)^5\)
\(=\left(\dfrac{7}{8}\cdot\dfrac{16}{21}\right)^5=\left(\dfrac{2}{3}\right)^5=\dfrac{32}{243}\)
8: \(\left(\dfrac{5}{6}\right)^4:\left(\dfrac{25}{18}\right)^4=\left(\dfrac{5}{6}:\dfrac{25}{18}\right)^4=\left(\dfrac{5}{6}\cdot\dfrac{18}{25}\right)^4=\left(\dfrac{3}{5}\right)^4=\dfrac{81}{625}\)
9:
\(\left(-\dfrac{3}{4}\right)^3:\left(\dfrac{9}{8}\right)^3=\left(-\dfrac{3}{4}:\dfrac{9}{8}\right)^3=\left(-\dfrac{3}{4}\cdot\dfrac{8}{9}\right)^3\)
\(=\left(-\dfrac{2}{3}\right)^3=-\dfrac{8}{27}\)
10:
\(\left(\dfrac{9}{10}\right)^6:\left(\dfrac{27}{-20}\right)^6=\left(\dfrac{9}{10}:\dfrac{-27}{20}\right)^6\)
\(=\left(\dfrac{9}{10}\cdot\dfrac{20}{-27}\right)^6=\left(-\dfrac{2}{3}\right)^6=\dfrac{64}{729}\)

a: góc BAH=90-50=40 độ
Xét ΔABM và ΔDCM có
AB=DC
góc ABM=góc DCM
MB=MC
Do đó: ΔABM=ΔDCM
b: ΔABM=ΔDCM
=>góc AMB=góc DMC
=>góc DMC+góc CMA=180 độ
=>A,M,D thẳng hàng
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>BD//AC

a: XétΔCHA vuông tại H và ΔCHD vuông tại H có
CH chung
HA=HD
=>ΔCHA=ΔCHD
=>CA=CD
b: DM vuông góc AC
AB vuông góc AC
=>DM//AB
=>góc HDK=góc HAB
Xét ΔHAB vuông tại H và ΔHDK vuông tại H có
HA=HD
góc HAB=góc HDK
=>ΔHAB=ΔHDK
=>HB=HK
=>H là trung điểm của BK
d: Xét ΔCAD có
AF.CH,MD là đường cao
=>AF,CH,MD đồng quy
=>A,K,F thẳng hàng

Tổng số phần bằng nhau: 3+5=8(phần)
Bạn Hùng quyên góp: 400 000 : 8 x 5 = 250 000 (đồng)
Bạn Minh quyên góp: 400 000 : 8 x 3 = 150 000 (đồng)
Bạn Dũng quyên góp: 400 000 : 8 x 4 = 200 000 (đồng)

a) \(\dfrac{3}{5}\times\dfrac{7}{9}+\dfrac{3}{5}\times\dfrac{2}{9}+\dfrac{-3}{5}\)
\(=\dfrac{3}{5}\times\dfrac{7}{9}+\dfrac{3}{5}\times\dfrac{2}{9}+\dfrac{3}{5}\times\left(-1\right)\)
\(=\dfrac{3}{5}\times\left(\dfrac{7}{9}+\dfrac{2}{9}-1\right)\)
\(=\dfrac{3}{5}\times\left(1-1\right)\)
\(=\dfrac{3}{5}\times0=0\)
b) \(\dfrac{2}{3}\cdot\dfrac{17}{13}-\dfrac{2}{3}\cdot\dfrac{4}{13}\)
\(=\dfrac{2}{3}\cdot\left(\dfrac{17}{13}-\dfrac{4}{13}\right)\)
\(=\dfrac{2}{3}\cdot1=\dfrac{2}{3}\)

a/\(-\dfrac{4}{3}x=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}:\left(-\dfrac{4}{3}\right)\)
\(x=-\dfrac{1}{4}\)
Vậy \(x=-\dfrac{1}{4}\)
b/\(\left|x-\dfrac{1}{2}\right|=\dfrac{5}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{5}{2}\\x-\dfrac{1}{2}=-\dfrac{5}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy \(x\in\left\{3;-2\right\}\)
\(a.-\dfrac{4}{3}x=\dfrac{1}{3}\)
\(\Leftrightarrow x=\dfrac{\dfrac{1}{3}}{\dfrac{-4}{3}}\)
\(\Leftrightarrow x=-\dfrac{1}{4}\)
Vậy \(x=-\dfrac{1}{4}\)
b)
\(\left|x-\dfrac{1}{2}\right|=\dfrac{5}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{5}{2}\\x-\dfrac{1}{2}=-\dfrac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{2}=3\\x=-\dfrac{4}{2}=-2\end{matrix}\right.\)
Vậy \(x\in\left\{-2;3\right\}\)




 Mng giúp mik vs ạ
Mng giúp mik vs ạ

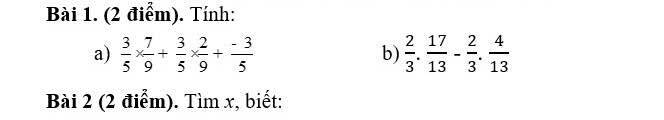

2:
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
ΔBAD cân tại B có BE là phân giác
nên BE vuông góc AD
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
AF=DC
=>ΔEAF=ΔEDC
=>EF=EC
=>ΔECF cân tại E
d: ΔEAF=ΔEDC
=>góc AEF=góc DEC
=>góc AEF+góc AED=180 độ
=>D,E,F thẳng hàng