
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)

\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2

Bài 2:
a) Để hàm số đồng biến thì m+1>0
hay m>-1
b) Để hàm số đi qua điểm A(2;4) thì
Thay x=2 và y=4 vào hàm số, ta được:
\(\left(m+1\right)\cdot2=4\)
\(\Leftrightarrow m+1=2\)
hay m=1
c) Để hàm số đi qua điểm B(2;-4) thì
Thay x=2 và y=-4 vào hàm số, ta được:
\(2\left(m+1\right)=-4\)
\(\Leftrightarrow m+1=-2\)
hay m=-3
Bài 1:
b) Ta có: \(5\cdot\sqrt{25a^2}-25a\)
\(=5\cdot5\cdot\left|a\right|-25a\)
\(=-25a-25a=-50a\)

Kẻ đường cao AH
Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Áp dụng HTL: \(BH=\dfrac{AB^2}{BC}=\dfrac{18}{5}\left(cm\right);AH=\dfrac{AB\cdot AC}{BC}=\dfrac{24}{5}\left(cm\right)\)
Vì AD là p/g nên \(\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow BD=\dfrac{3}{4}DC\)
Mà \(BD+DC=BC=10\Rightarrow\dfrac{7}{4}DC=10\Rightarrow DC=\dfrac{40}{7}\left(cm\right)\)
\(\Rightarrow BD=\dfrac{30}{7}\left(cm\right)\)
\(\Rightarrow HD=BD-BH=\dfrac{30}{7}-\dfrac{18}{5}=\dfrac{24}{35}\)
Áp dụng PTG: \(AD=\sqrt{AH^2+HD^2}=\sqrt{\left(\dfrac{24}{35}\right)^2+\left(\dfrac{24}{5}\right)^2}=\dfrac{24\sqrt{2}}{7}\approx4,85\left(cm\right)\)

Bài 2 :
a, Ta có đồ thị :
b, Ta có : \(\tan a=3\)
\(\Rightarrow a\approx71,5^o\)

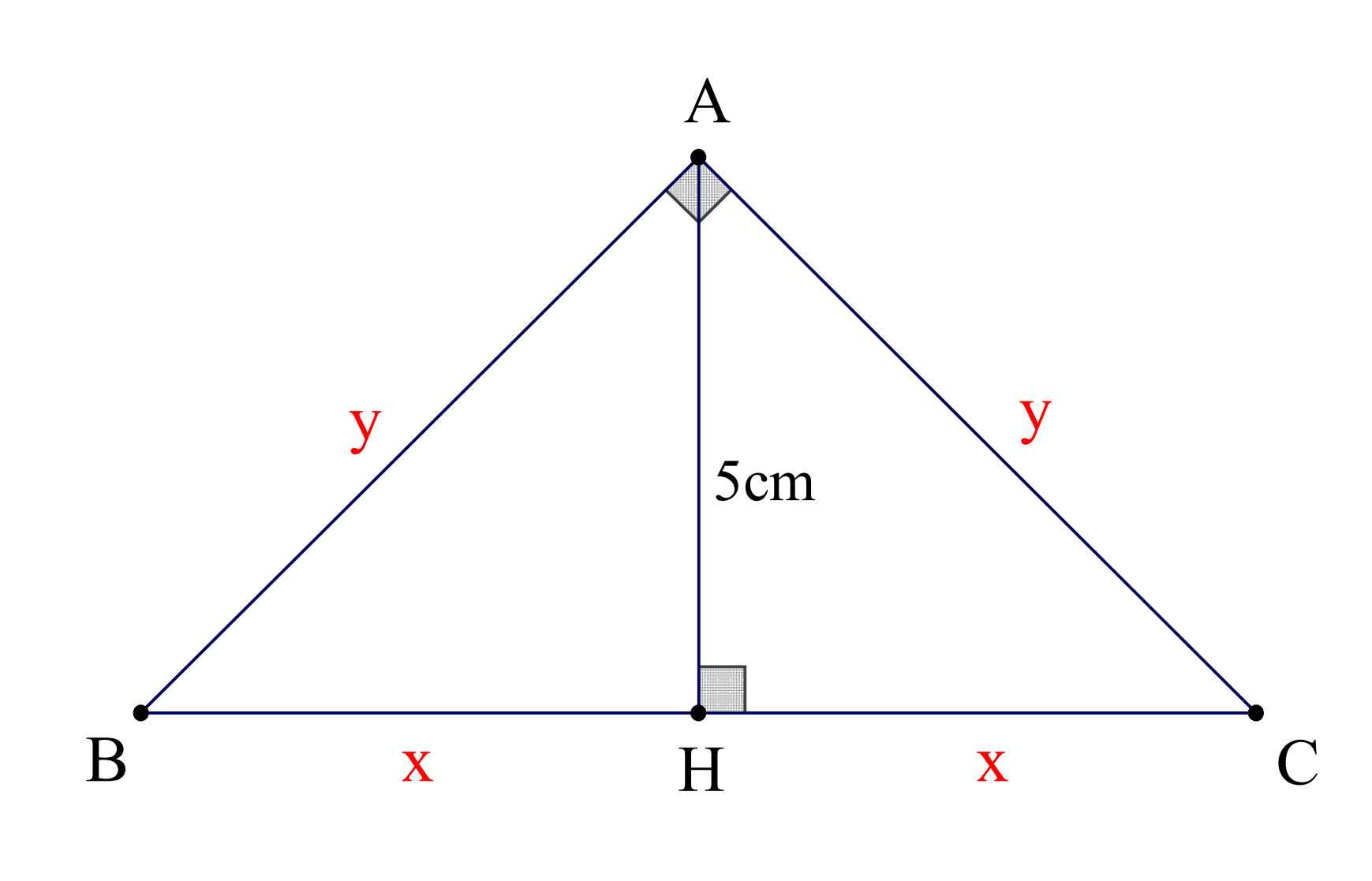
Áp dụng HTL trong tam giác ABC vuông tại A có đường cao AH:
\(AH^2=BH.HC\)
\(\Rightarrow x^2=5^2\Rightarrow x=5\left(cm\right)\)
\(AB^2=BH.BC\)
\(\Rightarrow AB=\sqrt{BH.BC}=\sqrt{5.\left(5+5\right)}\)
\(\Rightarrow y=5\sqrt{2}\left(cm\right)\)

\(a,A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)\left(1+\dfrac{1}{\sqrt{x}}\right)\left(dkxd:x\ge0,x\ne1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{2}{\sqrt{x}-1}\)
\(b,x=\dfrac{1}{4}\Rightarrow A=\dfrac{2}{\sqrt{\dfrac{1}{4}}-1}=\dfrac{2}{\dfrac{1}{2}-1}=-4\)
Vậy khi \(x=\dfrac{1}{4}\) thì \(A=-4\)
\(c,\sqrt{A}=A\Leftrightarrow\sqrt{\dfrac{2}{\sqrt{x}-1}}=\dfrac{2}{\sqrt{x}-1}\)
Bình phương 2 vế pt, ta có :
\(\dfrac{2}{\sqrt{x}-1}=\dfrac{4}{\left(\sqrt{x}-1\right)^2}\\ \Leftrightarrow\dfrac{2\left(\sqrt{x}-1\right)-4}{\left(\sqrt{x}-1\right)^2}=0\\ \Leftrightarrow2\sqrt{x}-2-4=0\\ \Leftrightarrow2\sqrt{x}=6\\ \Leftrightarrow\sqrt{x}=3\\ \Leftrightarrow x=9\)
a: ĐKXĐ: x>0; x<>1
\(A=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{x-1}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{1}{\sqrt{x}-1}=\dfrac{2}{\sqrt{x}-1}\)
b: Khi x=1/4 thì A=2:(1/2-1)=2:(-1/2)=-4
c: Để căn A=A thì A=0 hoặc A=1
=>căn x-1=0(loại) hoặc căn x-1=2/1=2
=>x=9

a: \(\text{Δ}=6^2-4\cdot3\cdot\left(-15\right)=36+180=216>0\)
Do đó:Phương trình có hai nghiệm phân biệt
\(x_1+x_2=\dfrac{-6}{3}=-2;x_1x_2=\dfrac{-15}{3}=-5\)
b: \(A=3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+4x_1x_2\)
\(=3\cdot\left[\left(-2\right)^2-2\cdot\left(-5\right)\right]+4\cdot\left(-5\right)\)
\(=3\left(4+10\right)-20=14\cdot3-20=22\)
a. \(\Delta=6^2-4.3.\left(-15\right)=36+180=216>0\)
Vậy phương trình luôn có 2 nghiệm phân biệt
Áp dụng định lí Vi-et có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-6}{3}=-2\\x_1x_2=\dfrac{-15}{4}=-5\end{matrix}\right.\)
b. Ta có: \(3x_1^2+4x_1x_2+3x_2^2=3\left(x_1+x_2\right)^2-2x_1x_2=3\left(-2\right)^2-2\left(-5\right)=22\)

a: Thay x=-2 vào \(\left(P\right)\), ta được:
\(y=\dfrac{1}{4}\cdot\left(-2\right)^2=1\)
Thay x=4 vào \(\left(P\right)\), ta được:
\(y=\dfrac{1}{4}\cdot4^2=4\)
Gọi \(\left(d\right):y=ax+b\)
Vì \(\left(d\right)\) đi qua hai điểm \(A\left(-2;1\right)\)và \(B\left(4;4\right)\) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6a=-3\\4a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=4-4a=4-4\cdot\dfrac{1}{2}=2\end{matrix}\right.\)
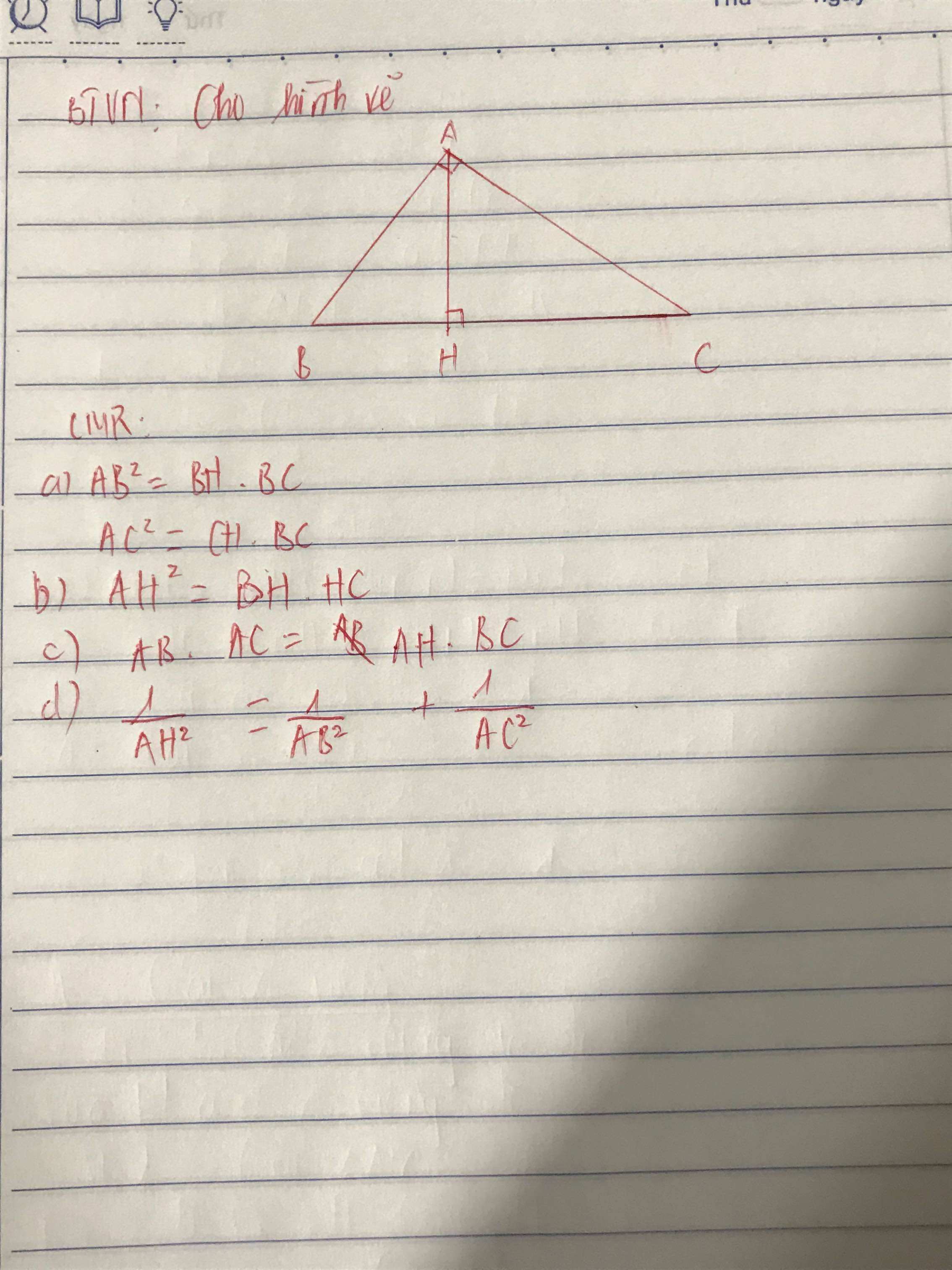






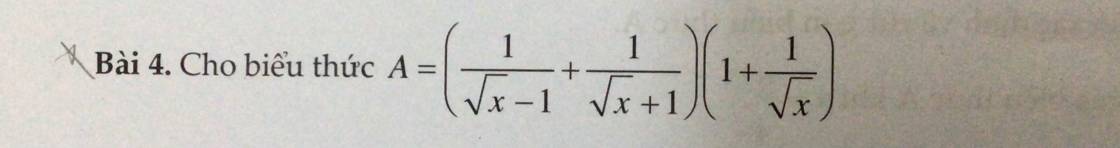
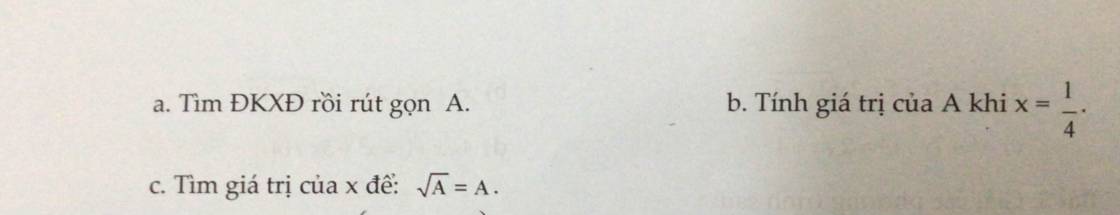


a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)
=>\(CH\cdot CB=CA^2\)
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
c: ΔCHA~ΔCAB
=>\(\dfrac{CA}{CB}=\dfrac{AH}{AB}\)
=>\(AB\cdot AC=AH\cdot BC\)
d: \(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{AB^2+AC^2}{AB^2\cdot AC^2}=\dfrac{BC^2}{BH\cdot BC\cdot CH\cdot BC}=\dfrac{1}{BH\cdot CH}=\dfrac{1}{AH^2}\)
a, Xét tam giác AHB và tam giác CAB có
^AHB = ^CAB ; ^ABH _ chung
Vậy tam giác AHB ~ tam giác CAB (g.g)
\(\dfrac{AB}{BC}=\dfrac{HB}{AB}\Rightarrow AB^2=HB.BC\)
tương tự tam giác AHC ~ tam giác CAB
\(\dfrac{AH}{AC}=\dfrac{AC}{BC}\Rightarrow AC^2=AH.BC\)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA ; ^ABH = ^CAH ( cùng phụ với ^BAH )
Vậy tam giác AHB ~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=HB.HC\)
c, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}AH.BC\Rightarrow AB.AC=AH.BC\)
d, Ta có \(AH^2=BH.CH\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{BH.CH}=\dfrac{BC^2}{AB^2.AC^2}=\dfrac{AB^2+AC^2}{AB^2.AC^2}=\dfrac{1}{AC^2}+\dfrac{1}{AB^2}\)