
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{2\left(x-2\right)}{x\left(x-2\right)}=\dfrac{2}{x}\)
\(a,=\dfrac{2\left(x-2\right)}{x\left(x-2\right)}=\dfrac{2}{x}\\ b,=\dfrac{\left(1-3x\right)\left(2x-1\right)+2x\left(3x-2\right)-\left(3x-2\right)}{2x\left(2x-1\right)}\\ =\dfrac{\left(1-3x\right)\left(2x-1\right)+\left(2x-1\right)\left(3x-2\right)}{2x\left(2x-1\right)}\\ =\dfrac{\left(2x-1\right)\left(1-3x+3x-2\right)}{2x}=\dfrac{-1}{2x}\)

Lời giải:
$(2x-3)(x^2+1)=0$
\(\Leftrightarrow \left[\begin{matrix} 2x-3=0\\ x^2+1=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{3}{2}(\text{chọn})\\ x^2=-1<0(\text{vô lý})\end{matrix}\right.\)
Vậy pt có nghiệm $x=\frac{3}{2}$

a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^3+3xy^2-4y-3xy^2=2x^3-4y\)

\(15x^2y^5-10x^3y^4=5x^2y^4\left(3y-2x\right)\)
\(4x\left(x-2y\right)+7\left(2y-x\right)=4x\left(x-2y\right)-7\left(x-2y\right)=\left(x-2y\right)\left(4x-7\right)\)
\(5x^3+20x^2y+20xy^2=5x\left(x^2+4xy+4y^2\right)=5x\left(x+2y\right)^2\)
\(x^2-4y^2-2x+4y=\left(x-2y\right)\left(x+2y\right)-2\left(x-2y\right)=\left(x-2y\right)\left(x+2y-2\right)\)

\(P=\dfrac{x}{2x-2}+\dfrac{x^2+1}{2-2x^2}\)
a: \(P=\dfrac{x}{2\left(x-1\right)}-\dfrac{x^2+1}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+x-x^2-1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{2\left(x+1\right)}\)
b: Để P=-1/2 thì 1/2(x+1)=-1/2
=>x+1=-1
=>x=-2

\(=\left(6x^3-10x^2-18x^2+30x+21x-35-5\right):\left(3x-5\right)\\ =\left[2x^2\left(3x-5\right)-6x\left(3x-5\right)+7\left(3x-5\right)-5\right]:\left(3x-5\right)\\ =2x^2-6x+7\left(\text{dư }-5\right)\)

a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^2y^2+3xy^2-4y-3xy^2=2x^2y^2-4y\)

\(8,=\left(2x-3\right)\left(2x+3\right)\\ 9,=\left(1-5a^2\right)\left(1+5a^2\right)\)
8) \(-9+4x^2=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
9) \(1-25a^4=1-\left(5a^2\right)^2=\left(1-5a^2\right)\left(1+5a^2\right)\)
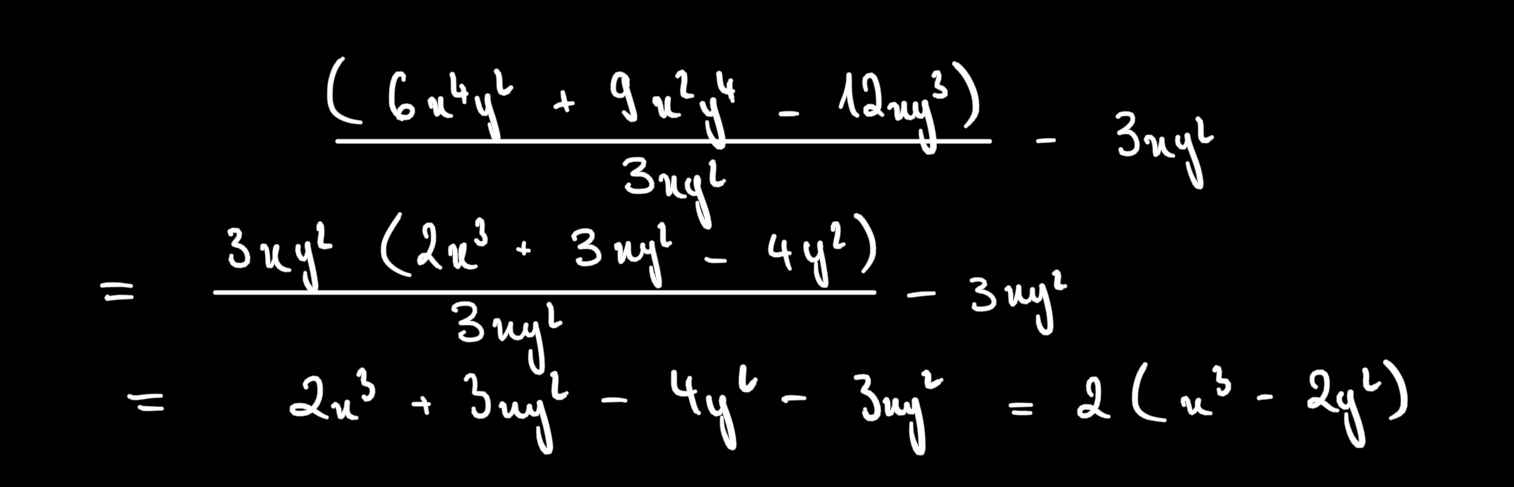



\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow\dfrac{2.\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}-\dfrac{1.\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow2x-4-x+1=3x-11\\ \Leftrightarrow x-3=3x-11\\ \Leftrightarrow x-3x=-11+3\\ \Leftrightarrow-2x=-8\\ \Leftrightarrow x=4\)
Vậy tập nghiệm của phương trình là S = { 4 }
thiếu điều kiện của x