Xét ΔPOQ có OP=OQ=PQ

nên ΔOPQ đều

=>góc POQ=60 độ

=>góc NOQ=30 độ

a: ΔOAB cân tại O

mà OI là đường trung tuyến

nên OI vuông góc AB

I là trung điểm của AB

=>IA=IB=16/2=8cm

ΔOIA vuông tại I

=>OA^2=OI^2+IA^2

=>OI^2=10^2-8^2=36

=>OI=6(cm)

b: OM=OI+IM

=>6+IM=10

=>IM=4cm

ΔMIA vuông tại I

=>MI^2+IA^2=MA^2

=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

Xét (O) có

ΔACB nội tiếp

AB là đường kính

=>ΔACB vuông tại C

ΔOCD cân tại O

mà OI là đường cao

nên I là trung điểm của CD

=>IC=ID=CD/2=8cm

Xét ΔCAB vuông tại C cso CI là đường cao

nên CI^2=IA*IB

=>8^2=6*IB

=>IB=64/6=32/3(cm)

AB=IB+IA=32/3+6=50/3(cm)

=>R=50/3:2=25/3(cm)

Vì OH vuông với AB => H là trung điểm 

=> AH = HB = AB/2 = 12/2 = 6 cm 

Theo định lí Pytago tam giác AHO vuông tại H ta được : 

\(AO=\sqrt{AH^2+OH^2}=\sqrt{64+36}=10\)cm 

hay R = 10 cm 

 Kéo dài HO về phía O cắt (o) tại K => KH là đường kính (o). Nối CH; CK ta có 

^KCH=90 (góc nội tiếp chắn nửa đường tròn)

CM=DM=CD/2=8 cm (bán kính vuông góc với dây cung thì chia đôi dây cung)

 Xét tg vuông KCH có \(CM^2=MH.MK\Rightarrow8^2=4.MK\Rightarrow MK=16cm\)

\(\Rightarrow KH=MH+MK=4+16=20cm\Rightarrow OK=\frac{KH}{2}=10cm\)

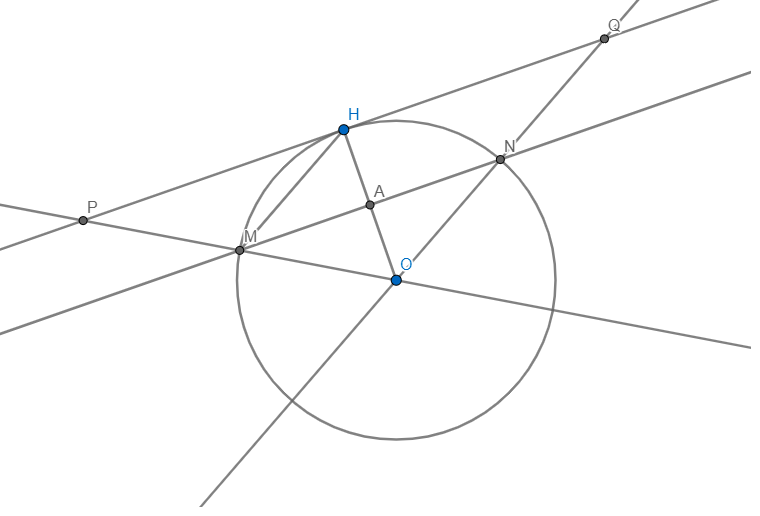
MN cắt OH tại A.

Vì MN là trung trực \(\Rightarrow MN\bot OH\) và A là trung điểm OH

mà \(PQ\bot OH\) \(\Rightarrow PQ\parallel MN\)

Xét \(\Delta OHQ\) có A là trung điểm OH và \(AN\parallel HQ\)

\(\Rightarrow N\) là trung điểm OQ

Tương tự \(\Rightarrow M\) là trung điểm OP

\(\Rightarrow MN\) là đường trung bình tam giác OPQ

\(\Rightarrow PQ=2MN\)

Vì MN là trung trực OH \(\Rightarrow MH=MO=OH\left(=R\right)\Rightarrow\Delta MOH\) đều

\(\Rightarrow MA=sinMHA.MH=sin60.R=\dfrac{\sqrt{3}}{2}R\Rightarrow MN=\sqrt{3}R\)

\(\Rightarrow PQ=2\sqrt{3}R\)

mình cảm ơn

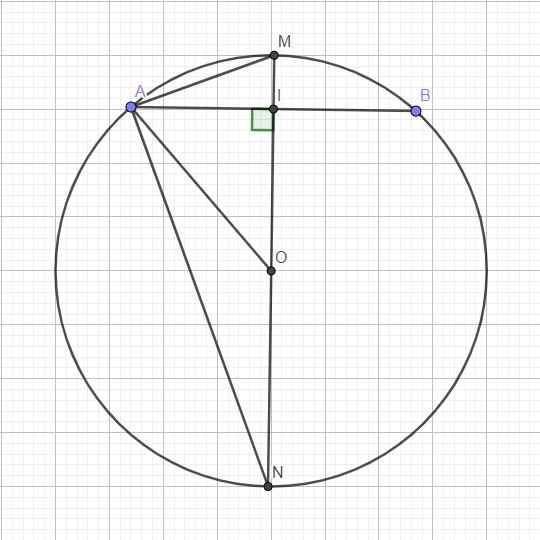
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)

\(AI=\dfrac{1}{2}AB=3\)

Trong tam giác vuông OAI, áp dụng Pitago:

\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)

\(\Rightarrow IM=OM-OI=R-OI=1\)

\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)

b.

Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)

Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A

Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:

\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)

Áp dụng hệ thức lượng:

\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)

\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)