
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-\left(2x+1\right)+2x+1-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-\dfrac{4x^2}{\sqrt{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\left(-\dfrac{4}{\sqrt{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-4}{1+1}+\dfrac{12}{1+1+1}=2\)

a/ \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt[3]{x^2-1}-2}{x-3}+\lim\limits_{x\rightarrow3}\dfrac{2-\sqrt[4]{1+5x}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^2-1-8}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{16-1-5x}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4.\sqrt[3]{1+5x}+8\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{-5\left(x-3\right)}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4\sqrt[3]{1+5x}+8\right)}\)
\(=\dfrac{3+3}{\sqrt[3]{\left(3^2-1\right)^2}+2.\sqrt[3]{3^2-1}+4}-\dfrac{5}{\sqrt[4]{\left(1+5.3\right)^3}+2\sqrt[3]{\left(1+5.3\right)^2}+4.\sqrt[3]{1+5.3}+8}=\dfrac{11}{32}\)
\(\Rightarrow a^2+b^2=1145\)
40/
\(L=\lim\limits_{x\rightarrow0}\dfrac{af\left(x\right)+b^n-b^n}{f\left(x\right)\left[\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+....+b^{n-1}\right]}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+...+b^{n-1}}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{b^{n-1}+b^{n-1}++...+b^{n-1}}=\dfrac{a}{nb^{n-1}}\)

Đặt \(cosx-sinx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1-2sinx.cosx\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Pt trở thành:
\(t\left(1+\dfrac{1-t^2}{2}\right)+1=0\)
\(\Leftrightarrow t^3-3t-2=0\)
\(\Leftrightarrow\left(t-2\right)\left(t+1\right)^2=0\Rightarrow\left[{}\begin{matrix}t=2\left(loại\right)\\t=-1\end{matrix}\right.\)
\(\Rightarrow cosx-sinx=-1\)
\(\Leftrightarrow\sqrt[]{2}cos\left(x+\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=cos\left(\dfrac{3\pi}{4}\right)\)
\(\Leftrightarrow...\)

Bạn kiểm tra lại đề bài câu a, n=1 thì VT=1, VP=-1, nếu đề bài đúng thì vp phải là \(\dfrac{-\left(1\right)^{n-1}n\left(n+1\right)}{2}\)
\(n=1\Rightarrow VT=1=VP\)
Vậy mệnh đề đúng với n=1
Giả sử mệnh đề cũng đúng với \(n=k\left(k\in N\right)\), hay:
\(1^2-2^2+...+\left(-1\right)^{k-1}.k^2=\dfrac{\left(-1\right)^{k-1}.k.\left(k+1\right)}{2}\)
Ta cần chứng minh mệnh đề cũng đúng với \(n=k+1\) ,hay:
\(1^2-2^2+...+\left(-1\right)^{k-1}.k^2+\left(-1\right)^k.\left(k+1\right)^2=\dfrac{\left(-1\right)^k.\left(k+1\right)\left(k+2\right)}{2}\)
That vay:
\(VT=\dfrac{\left(-1\right)^{k-1}k\left(k+1\right)}{2}+\left(-1\right)^k.\left(k+1\right)^2=\dfrac{\left(-1\right)^{k-1}.k.\left(k+1\right)+2\left(-1\right)^k\left(k+1\right)^2}{2}\)
\(=\dfrac{\left(-1\right)^k\left(k+1\right)\left(-k+2k+2\right)}{2}=\dfrac{\left(-1\right)^k\left(k+1\right)\left(k+2\right)}{2}=VP\)
Vậy mệnh đề đúng với \(\forall n\in N\)
b/ \(n=7\Rightarrow VT=3^7=2187< 7!=5040\)
Vậy mệnh đề đúng với n=7
Giả sử mệnh đề đúng với \(n=k\left(k\in N;k\ge7\right)\),hay:
\(3^k\le k!\)
Ta cần chứng minh mệnh đề cũng đúng với \(n=k+1\) ,hay:
\(3^{k+1}\le\left(k+1\right)!\)
That vay:
\(3^k.3\le\left(k+1\right).k!\)
\(k>6\Rightarrow k+1>6\Rightarrow k+1>3\)
Ma \(3^k\le k!\)
\(\Rightarrow3^k.3\le\left(k+1\right).k!\Leftrightarrow3^{k+1}\le\left(k+1\right)!\)
Vậy mệnh đề đúng với \(\forall n\in N;n>6\)

sinx - sin3x - \(\sqrt{3}\left(cosx+sin3x\right)=0\)
⇔ sinx - \(\sqrt{3}cosx-\left(1+\sqrt{3}\right)sin3x\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)-\left(1-\sqrt{3}\right)sin\left(\pi-3x\right)\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin\left(3x-\pi\right)=0\)
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin3\left(x-\dfrac{\pi}{3}\right)=0\)
Đặt a = x - \(\dfrac{\pi}{3}\) ta có phương trình mới
2sina + (1 - \(\sqrt{3}\))sin3a = 0 (1)
Sử dụng công thức sin3a = 3sina - 4sin3a đưa (1) về phương trình bậc 3 ẩn là a. Từ a suy ra x


21.
Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx+2\right)}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=\dfrac{-b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
\(\Rightarrow a+b=1-8=-7\)
22.
B sai, do các cạnh bên của chóp đều tạo với đáy các góc bằng nhau





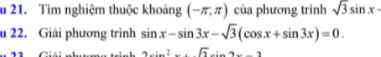



\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{x+2017-\left(2015-x\right)}{\sqrt[3]{\left(x+2017\right)^2}+\sqrt[3]{\left(x+2017\right)\left(2015-x\right)}+\sqrt[3]{\left(2015-x\right)^2}}}{\dfrac{2000+x-\left(1998-x\right)}{\sqrt{2000+x}+\sqrt{1998-x}}}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\sqrt{2000+x}+\sqrt{1998-x}}{\sqrt[3]{\left(x+2017\right)^2}+\sqrt[3]{\left(x+2017\right)\left(2015-x\right)}+\sqrt[3]{\left(2015-x\right)^2}}\)
\(=\dfrac{\sqrt{1999}+\sqrt{1999}}{\sqrt[3]{2016^2}+\sqrt[3]{2016^2}+\sqrt[3]{2016^2}}=\dfrac{2\sqrt{1999}}{3.24\sqrt[3]{294}}=\dfrac{\sqrt{1999}}{36\sqrt[3]{294}}\)
\(\Rightarrow a+b=1999+294\)