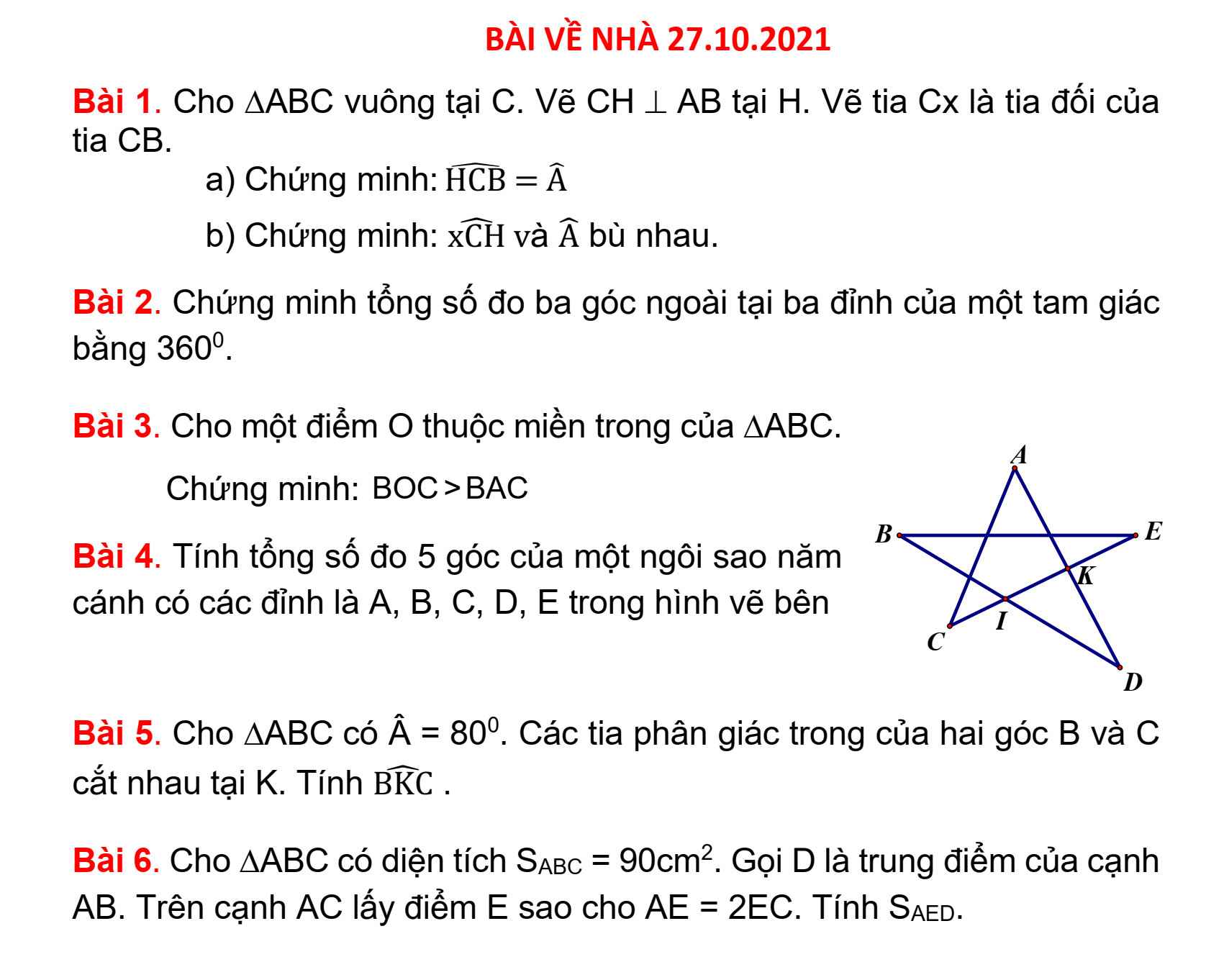
Bài 5: 

\(\widehat{BKC}=180^0-\left(\widehat{KBC}+\widehat{KCB}\right)\)

\(=180^0-\dfrac{180^0-80^0}{2}\)

\(=180^0-50^0=130^0\)

Đặt A = 1+2+2^2+2^3+....+2^60

2A = 2+2^2+2^3+2^4+.....+2^61

2A-A= ( 2+2^2+2^3+....+2^61)-(1+2+2^2+.....+2^60)

A = 2^61-1

http://olm.vn/hoi-dap/question/232902.html

tự giải đi em bài này học sinh trường chị biết giải hết đó:v

. Đ biết giải mới hỏi chứ =)) Em học ngu lắm =)) 

Giải:

Ta có:

\(\widehat{O_2}+\widehat{O_1}=180^o\) ( kề bù ) và \(\widehat{O_2}-\widehat{O}_1=10^o\)

\(\Rightarrow\widehat{O_1}=\left(180^o-10^o\right):2=85^o\)

\(\Rightarrow\widehat{O}_2=85^o+10^o=95^o\)

\(\Rightarrow\widehat{O_1}=\widehat{O_3}=85^o\) ( đối đỉnh )

\(\Rightarrow\widehat{O}_2=\widehat{O_4}=95^o\) ( đối đỉnh )

Vậy \(\widehat{O_1}=85^o;\widehat{O_2}=95^o;\widehat{O_3}=85^o;\widehat{O_4}=95^o\)

cảm ơn bạn nhiều

đề thiếu cái gì đó thì phải
 

Vế phải = 0 ?

\(\Leftrightarrow2x^2-2x-5x+5=0\)

\(\Leftrightarrow2x\left(x-1\right)-5\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(2x-5\right)=0\)

\(\Leftrightarrow\hept{\begin{cases}2x-5=0\\x-1=0\end{cases}}\)

Rồi giải nốt đi

Bài `3`

Cậu tách cho các câu sau nx nhé^^

\(a,x+\dfrac{1}{2}=\dfrac{7}{3}\\ \Rightarrow x=\dfrac{7}{3}-\dfrac{1}{2}\\ \Rightarrow x=\dfrac{14}{6}-\dfrac{3}{6}\\ \Rightarrow x=\dfrac{11}{6}\\ b,\dfrac{2}{5}x-\dfrac{1}{5}=-0,6\\ \Rightarrow\dfrac{2}{5}x=-\dfrac{3}{5}+\dfrac{1}{5}\\ \Rightarrow\dfrac{2}{5}x=-\dfrac{2}{5}\\ \Rightarrow x=-\dfrac{2}{5}:\dfrac{2}{5}\\ \Rightarrow x=-1\\ c,\left(0,5x-\dfrac{3}{7}\right):\dfrac{1}{2}=1\dfrac{1}{7}\\ \Rightarrow\dfrac{1}{2}x-\dfrac{3}{7}=\dfrac{8}{7}\cdot\dfrac{1}{2}\\ \Rightarrow\dfrac{1}{2}x-\dfrac{3}{7}=\dfrac{8}{14}\\ \Rightarrow\dfrac{1}{2}x=\dfrac{4}{7}+\dfrac{3}{7}\\ \Rightarrow\dfrac{1}{2}x=1\\ \Rightarrow x=1:\dfrac{1}{2}\\ \Rightarrow x=2\)

\(d,\dfrac{2}{3}x-\dfrac{2}{5}=\dfrac{1}{2}x-\dfrac{1}{3}\\ \Rightarrow\dfrac{2}{3}x-\dfrac{1}{2}x=-\dfrac{1}{3}+\dfrac{2}{5}\\ \Rightarrow\left(\dfrac{2}{3}-\dfrac{1}{2}\right)x=\dfrac{1}{15}\\ \Rightarrow\dfrac{1}{6}x=\dfrac{1}{15}\\ \Rightarrow x=\dfrac{1}{15}:\dfrac{1}{6}\\ \Rightarrow x=\dfrac{2}{5}\)

`e,1/2 x+2 1/2=3 1/2 x-3/4`

`=> 1/2 x+ 5/2= 7/2x - 3/4`

`=> 1/2x - 7/2x = -3/4 -5/2`

`=> -3x=-13/4`

`=>x=13/12`

\(f,2x\left(x-\dfrac{1}{7}\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x-\dfrac{1}{7}=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{7}\end{matrix}\right.\\ g,\left(\dfrac{2x}{5}-1\right):\left(-5\right)=\dfrac{1}{4}\\ \Rightarrow2x:5-1=\dfrac{1}{4}\cdot\left(-5\right)\\ \Rightarrow2x:5-1=-\dfrac{5}{4}\\ \Rightarrow2x:5=-\dfrac{5}{4}+1\\ \Rightarrow2x:5=-\dfrac{1}{14}\\ \Rightarrow2x=-\dfrac{1}{14}\cdot5\\ \Rightarrow2x=-\dfrac{5}{14}\\ \Rightarrow x=-\dfrac{5}{14}:2\\ \Rightarrow x=-\dfrac{5}{28}\)

\(\left(x-1\right)^3=\dfrac{1}{8}\\ \Rightarrow\left(x-1\right)^3=\left(\dfrac{1}{2}\right)^3\\ \Rightarrow x-1=\dfrac{1}{2}\\ \Rightarrow x=\dfrac{1}{2}+1\\ \Rightarrow x=\dfrac{1}{2}+\dfrac{2}{2}\\ \Rightarrow x=\dfrac{3}{2}\)

mà cậu ơi làm cho mình mấy câu lũy thừa trên với ạ

\(A=3^{n+3}+3^{n-1}+2^{n+2}+2^{n+1}\)

\(=3^n\cdot\left(27+\dfrac{1}{3}\right)+2^n\left(4+2\right)\)

\(=3^{n-1}\cdot2\cdot41+2^n\cdot6⋮6\)