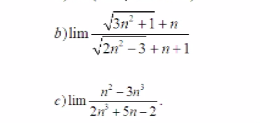b.

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)

\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)

c.

\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)

\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)

2.

\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)

\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)

\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)

Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)

\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)

\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)

12.

\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)

\(\Rightarrow M=\sqrt{2}\)

13.

Pt có nghiệm khi:

\(5^2+m^2\ge\left(m+1\right)^2\)

\(\Leftrightarrow2m\le24\)

\(\Rightarrow m\le12\)

14.

\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow x=k2\pi\)

15.

\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)

Đáp án A

16.

\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)

\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)

Có \(1008+1008=2016\) nghiệm

Trong mp (ABCD) từ A kẻ \(AE\perp BD\), trong mp (SAE) từ A kẻ \(AF\perp SE\) (1)

Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AE\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAE\right)\)

\(\Rightarrow BD\perp AF\) (2)

(1);(2) \(\Rightarrow AF\perp\left(SBD\right)\Rightarrow AF=d\left(A;\left(SBD\right)\right)\)

\(\lim\dfrac{\sqrt{3n^2+1}+n}{\sqrt{2n^2-3}+n+1}=\lim\dfrac{n\sqrt{3+\dfrac{1}{n^2}}+n}{n\sqrt{2-\dfrac{3}{n^2}}+n+1}\)

\(=\lim\dfrac{n\left(\sqrt{3+\dfrac{1}{n^2}}+1\right)}{n\left(\sqrt{2-\dfrac{3}{n^2}}+1+\dfrac{1}{n}\right)}=\lim\dfrac{\sqrt{3+\dfrac{1}{n^2}}+1}{\sqrt{2-\dfrac{3}{n^2}}+1+\dfrac{1}{n}}=\dfrac{\sqrt{3}+1}{\sqrt{2}+1}\)

Câu nào bạn, nếu mà cả thì đăng tách ra đi :)

Ok bạn =))