
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a,` ĐKXĐ: `x>=0;x\ne1`
`A=...=(sqrtx(1+sqrtx)+sqrtx(1-sqrtx)+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(sqrtx+x+sqrtx-x+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(3sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=-3/(1+sqrtx)`
`b,A=-3/(1+sqrtx)`
Vì `x>=0` nên `1+sqrtx>=1` nên `3/(1+sqrtx)<=3` suy ra `A>=-3`
Dấu "=" xảy ra `<=>x=0`
Vậy `A_(min)=-3<=>x=0`

a: ĐKXĐ: a>0; a<>1
\(A=\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\cdot\dfrac{a}{\sqrt{a}+1}=\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{a}{\sqrt{a}+1}\)
\(=\sqrt{a}\left(\sqrt{a}-1\right)=a-\sqrt{a}\)
b: A=a-căn a+1/4-1/4
=(căn a-1/2)^2-1/4>=-1/4
Dấu = xảy ra khi a=1/4

3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM

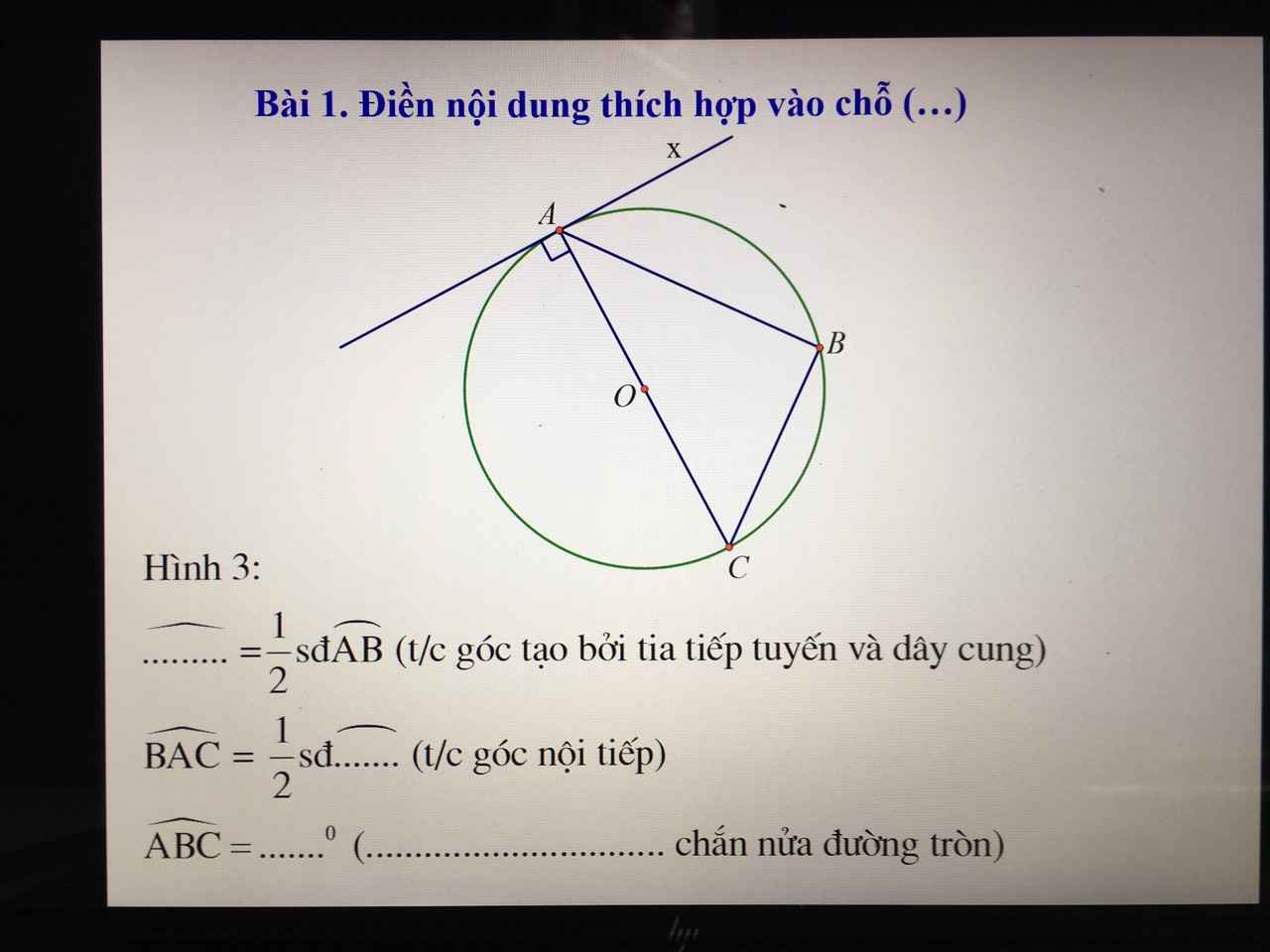
\(\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
\(\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\)
\(\widehat{ABC}=90^0\) (góc nội tiếp chắn nửa đường tròn)

Độ dài ACACAC được tính từ góc A=6∘A = 6^\circA=6∘ và cạnh đối AH=305 mAH = 305 \, mAH=305m.
AC=AHsinA=305sin6∘AC = \frac{AH}{\sin A} = \frac{305}{\sin 6^\circ}AC=sinAAH=sin6∘305Độ dài CBCBCB được tính từ góc B=4∘B = 4^\circB=4∘ và cạnh đối HB=458 mHB = 458 \, mHB=458m.
CB=HBsinB=458sin4∘CB = \frac{HB}{\sin B} = \frac{458}{\sin 4^\circ}CB=sinBHB=sin4∘458Thời gian leo dốc từ AAA đến CCC:
tAC=AC4 km/ht_{AC} = \frac{AC}{4 \, km/h}tAC=4km/hACThời gian xuống dốc từ CCC đến BBB:
tCB=CB19 km/ht_{CB} = \frac{CB}{19 \, km/h}tCB=19km/hCBTổng thời gian di chuyển: ttotal=tAC+tCBt_{\text{total}} = t_{AC} + t_{CB}ttotal=tAC+tCBThời gian bạn Học đến trường bằng cách cộng tổng thời gian này vào thời gian khởi hành 6 giờ 45 phút.

2: Để (d)//y=(m2+1)x-4 thì \(\left\{{}\begin{matrix}m^2=1\\m-5\ne-4\end{matrix}\right.\Leftrightarrow m=1\)

Gọi x(km/h) là vận tốc của ô tô thứ nhất (x>12)
Thời gian ô tô thứ nhất đi từ A đến B là 120/x (giờ)
Mỗi giờ ô tô thứ nhất chạt nhanh hơn ô tô thứ 2 là 12km/h=> vận tốc của ô tô thứ 2 là x-12 (km/h)
Thời gian ô tô thứ 2 đi từ A đến B là 120/(x-12)
Ô tô thứ nhất đến B trước ô tô thứ 2 là 30phút nên ta có phương trình:
120/x + 1/2 = 120/(x-12)
<=> 240x-2880=120x+240
<=> 120x=3120
<=> x=26 (t/m)
Vậy vận tốc của ô tô thứ nhất là 26km/h

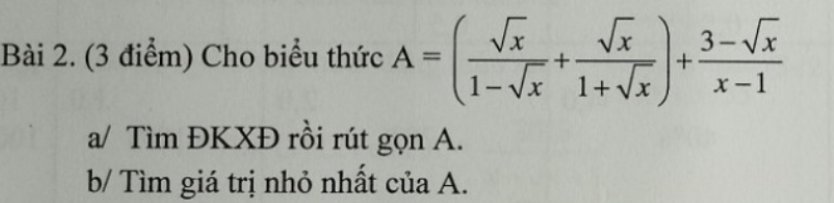
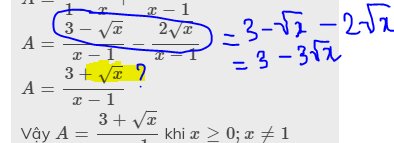
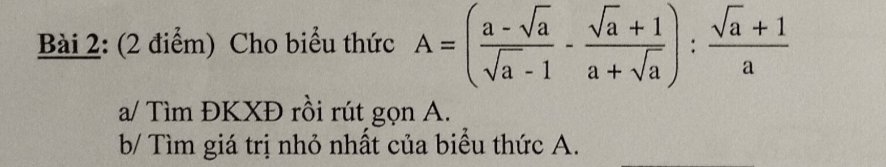





Lời giải:
a. Vì hệ số góc $2>0$ nên hàm số đồng biến trên $R$
b. Đồ thị $y=2x-3$ như sau:
c. Để hai đt đã cho cắt nhau thì $2\neq m+1$
$\Leftrightarrow m\neq 1$
Vạy $m\neq \pm 1$ để 2 đt cắt nhau.