6.

\(0,3a^3b^2\sqrt{\dfrac{9}{a^4b^8}}=0,3a^3b^2.\dfrac{3}{a^2b^4}=\dfrac{0,9.a}{b^2}\)

Đáp án B

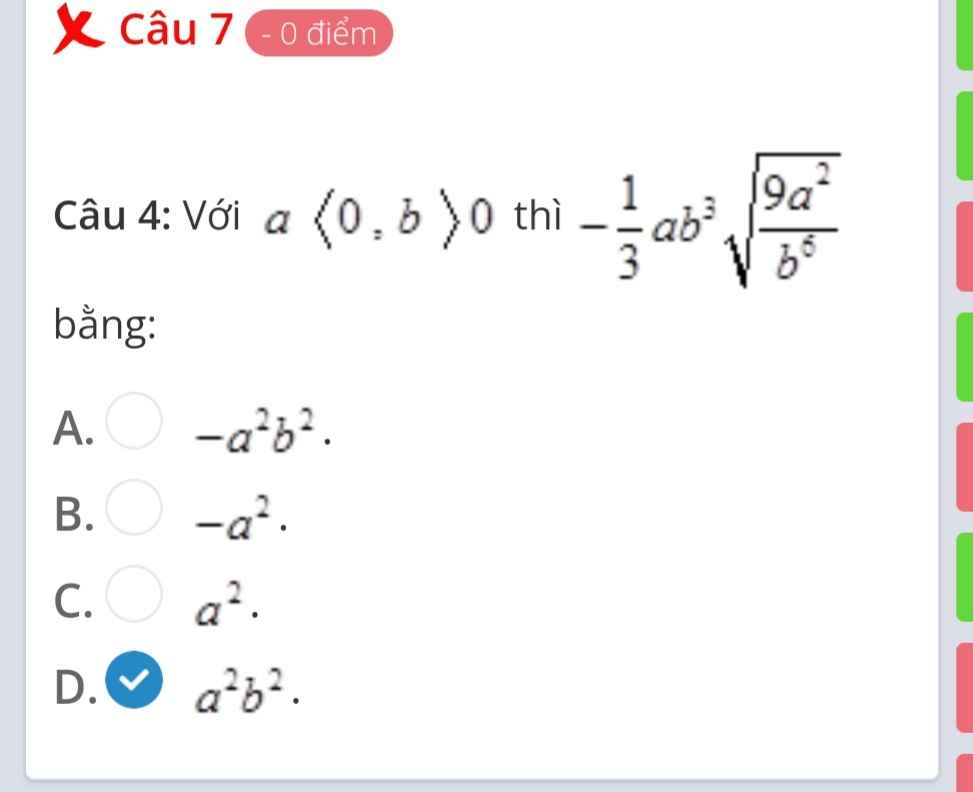
7.

\(-\dfrac{1}{3}ab^3\sqrt{\dfrac{9a^2}{b^6}}=-\dfrac{1}{3}ab^3.\dfrac{3\left|a\right|}{\left|b^3\right|}=-ab^3.\dfrac{-a}{b^3}=a^2\)

Đáp án C

Dạ em cảm ơn nhiều ạ

a: Xét tứ giác ADME có 

\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)

Do đó: ADME là hình chữ nhật

Lời giải:
Gọi số thứ nhất là $a$ và số thứ hai là $b$.

Theo bài ra ta có:
\(\left\{\begin{matrix} 4b+5a=18040\\ 3a-2b=2002\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5a+4b=18040\\ 6a-4b=4004\end{matrix}\right.\)

\(\Rightarrow 5a+6a=18040+4004\)

\(\Leftrightarrow 11a=22044\Leftrightarrow a=2004\)

\(b=\frac{3a-2002}{2}=2005\)

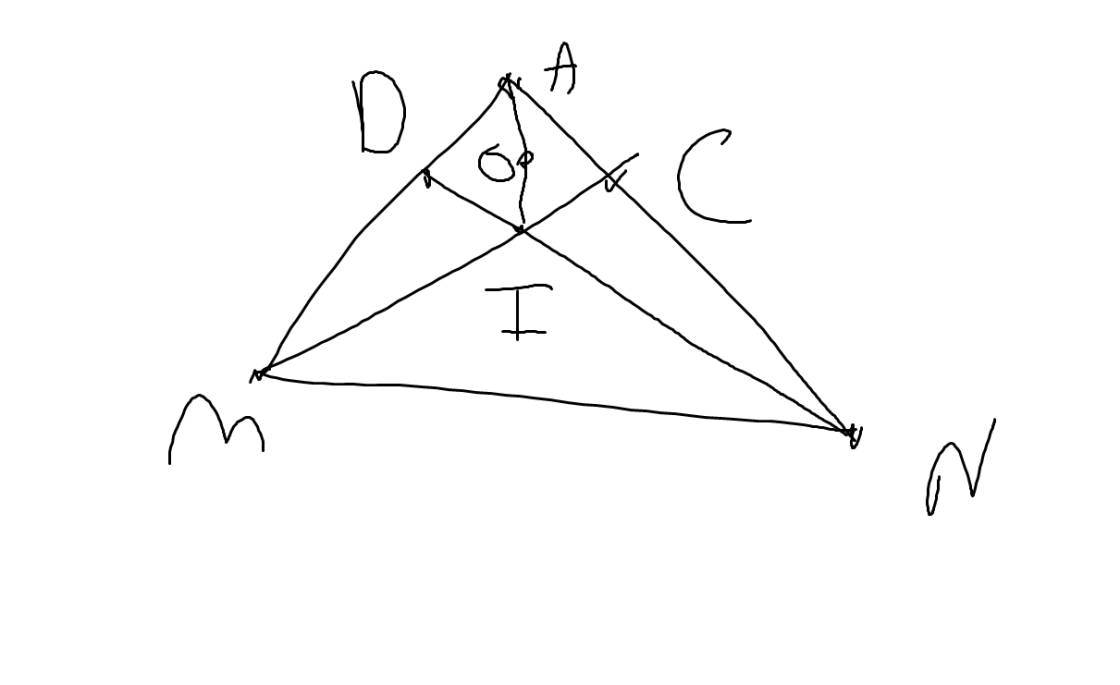
a: Sửa đề: Hai đường cao MC và ND cắt nhau tại I

Xét tứ giác MDCN có \(\widehat{MDN}=\widehat{MCN}=90^0\)

nên MDCN là tứ giác nội tiếp

=>M,D,C,N cùng thuộc một đường tròn

b: Xét tứ giác ADIC có

\(\widehat{ADI}+\widehat{ACI}=90^0+90^0=180^0\)

=>ADIC là tứ giác nội tiếp đường tròn đường kính AI

=>A,D,I,C cùng thuộc đường tròn đường kính AI

Tâm O là trung điểm của AI

Lên mạng coi

Đánh câu hỏi dàn ý vào goodle biết ngay mà.

Câu 1: A

Câu 2: D

Câu 3: B

Câu 4: C

Bài 1:

a) 

\(A=\left(\frac{4\sqrt{x}}{\sqrt{x}+2}-\frac{8x}{(\sqrt{x}-2)(\sqrt{x}+2)}\right):\left(\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}-\frac{2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}\right)\)

\(=\frac{4\sqrt{x}(\sqrt{x}-2)-8x}{(\sqrt{x}-2)(\sqrt{x}+2)}:\frac{\sqrt{x}-1-2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}=\frac{-4x-8\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{-\sqrt{x}+3}\)

\(=\frac{-4\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{3-\sqrt{x}}=\frac{-4x(\sqrt{x}-2)}{(\sqrt{x}-2)(3-\sqrt{x})}=\frac{4x}{\sqrt{x}-3}\)

b)

Ta có:
\(m(\sqrt{x}-3).A>x+2025\)

\(\Leftrightarrow 4xm>x+2025\Leftrightarrow x(4m-1)>2025\)

\(\Leftrightarrow 4m-1>\frac{2025}{x}\Leftrightarrow m>\frac{1}{4}(\frac{2025}{x}+1)\) với mọi $x>9$

\(\Leftrightarrow m> \max \frac{1}{4}(\frac{2025}{x}+1), \forall x>9\Leftrightarrow m>56,5\)

Đặt\(\begin{cases} x+y=S \\ xy=P \end{cases}\)

Ta có:\(\begin{cases} S-2P=0 \\ S-P^2=\sqrt{(P-1)^2+1} \end{cases}\)

\(\Leftrightarrow\)\(\begin{cases} S=2P \\ 2P-P^2=\sqrt{(P-1)^2+1} \end{cases}\)

\(\Leftrightarrow\)\(\begin{cases} S=2P \\ (2P-P^2)^2=(P-1)^2+1 \end{cases}\)

\(\Leftrightarrow\)\(\begin{cases} S=2P \\ 4P^2-4P^3+P^4=P^2-2P+2 \end{cases}\)

\(\Leftrightarrow\)\(\begin{cases} S=2P \\ P^4-4P^3+3P^2+2P-2=0 \end{cases}\)

\(\Leftrightarrow\)\(\begin{cases} S =2+2\sqrt{3}\\ P=1+\sqrt{3} \end{cases}\)(1)hoặc\(\begin{cases} S=2 \\ P=1 \end{cases}\)(2)hoặc\(\begin{cases} S=2-2 \sqrt{3}\\ P=1-\sqrt{3} \end{cases}\)(3)

Còn lại là thay vào biểu thức x²-Sx+P=0 thôi

Gọi tuổi của Bố và của Minh hiện nay lần lượt là x(tuổi) và y(tuổi)

(Điều kiện: x>0 và y>0)

Tổng số tuổi của hai người là 55 tuổi nên x+y=55(1)

Sau 10 năm nữa thì tuổi của bố là x+10(tuổi)

Sau 10 năm nữa thì tuổi của Minh là y+10(tuổi)

Sau 10 năm nữa thì tuổi bố gấp đôi tuổi Minh là:

x+10=2(y+10)

=>x+10=2y+20

=>x-2y=10(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}x+y=55\\x-2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=45\\x+y=55\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=15\\x=55-y=55-15=40\end{matrix}\right.\left(nhận\right)\)

Vậy: Hiện nay bố 40 tuổi và Minh 15 tuổi