Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
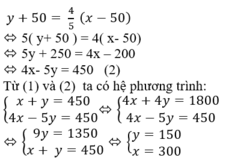
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
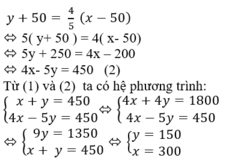
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Sau khi chuyển thì tổng số sách không đổi.
Sau khi chuyển nếu số sách ở ngăn thứ hai là \(4\)phần thì số sách ở ngăn thứ nhât là \(5\)phần.
Tổng số phần bằng nhau là:
\(4+5=9\)(phần)
Sau khi chuyển số sách ở ngăn thứ hai là:
\(450\div9\times4=200\)(cuốn)
Số sách ở ngăn thứ hai lúc đầu là:
\(200-50=150\)(cuốn)
Số sách ở ngăn thứ nhất lúc đầu là:
\(450-150=300\)(cuốn)
Sau khi chuyển thì tổng số sách hai ngăn không thay đổi.
Ta có sơ đồ :
Ngăn thứ nhất : |-----|-----|-----|-----|-----|
Ngăn thứ hai : |-----|-----|-----|-----|
Tổng số phần bằng nhau là :
4 + 5 = 9 ( phần )
Ngăn thứ hai chứa số sách lúc đầu là :
450 : 9 × 4 - 50 = 150 ( cuốn )
Ngăn thứ nhất chứa số sách lúc đầu là :
450 - 150 = 300 ( cuốn )
Đáp số : Ngăn thứ hai : 150 cuốn sách
Ngăn thứ nhất : 300 cuốn sách

Gọi x (cuốn) là số cuốn sách ở giá thứ nhất. ĐK: 450>x>50; \(x\in N\)
--> 450-x (cuốn) là số cuốn sách ở giá thứ hai
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách của giá thứ nhất lúc này là x-50 ( cuốn) và giá thứ hai là 500-x ( cuốn)
Khi đó số sách ở giá thứ hai bằng 4/5 số sách ở giá thứ nhất nên ta có pt:
\(500-x=\dfrac{4}{5}\left(x-50\right)\)
\(\Leftrightarrow500-x=\dfrac{4}{5}x-40\Leftrightarrow\dfrac{9}{5}x=540\Leftrightarrow x=300\)(tm)
Vậy số sách ở giá thứ nhất là 300 cuốn ; số sách ở giá thứ hai là 150 cuốn

gọi số sách lúc đầu ở giá 1 là x (cuốn)
ở giá 2 là y (cuốn)
Ta có phương trình tổng số sách ở 2 giá là x+ y = 450 (1)
theo đề bài ta có phương trình thứ hai là y + 50 = 4/5 (x-50) => 5(y+50) = 4(x-50) => 4x -5y = 450 (2)
giải hpt (1)(2) => x = 150; y = 300
Vậy số sách lúc đầu ở giá 1 là 150 ; giá 2 là 300 cuốn

| giá thứ 1 | giá thứ 2 | |
| lúc đầu | x | 450-x |
| lúc sau | x-50 | 450-x+50 |
tự lí luận nha...mk ko có t/g...
theo bài ra ta có pt
450-x+50=0,8(x-50)
=>500-x=0,8x-40
=>540=1,8x
=>x=300
giá thứ 2 lúc đầu có là
450-300=150 (qu)
vậy giá 1 lúc đầu có 300 quyển
giá 2 lúc đầu có là: 150 quyển
Ai h mk mk se h lại
Ngăn thứ nhất là : 300 quyển sách
Ngăn thứ hai là : 150 quyển sách

Gọi số sách trên hai giá lần lượt là x, y (0 < x, y < 450, cuốn)
Vì hai giá sách có 450 cuốn nên ta có phương trình: x + y = 450 (cuốn)
Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng 4 5 số sách ở giá thứ nhất nên ta có pt y + 50 = 4 5 x − 50
Suy ra hệ phương trình x + y = 450 y + 50 = 4 5 x − 50
⇔ x + y = 450 4 5 x − y = 90 ⇔ x = 300 y = 150 (thỏa mãn)
Vậy số sách trên giá thứ nhất là 300 cuốn, số sách trên giá thứ hai là 150 cuốn.
Đáp án: A

Gọi số sách trên 2 giá lúc đầu lần lượt là x và y cuốn (với x>100, y>0)
Do hai giá có tất cả 1820 cuốn sách nên: \(x+y=1820\)
Sau khi chuyển từ giá thứ nhất sang giá thứ hai 100 cuốn (đồng nghĩa giá thứ nhất giảm 100 cuốn và giá thứ hai tăng 100 cuốn) thì số sách 2 giá bằng nhau nên:
\(x-100=y+100\Rightarrow x-y=200\)
Ta được hệ:
\(\left\{{}\begin{matrix}x+y=1820\\x-y=200\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1010\\y=810\end{matrix}\right.\)
giúp mình cả lời giải nữa với