
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

Gọi chiều dài chiều rộng lần lượt là x ; y ( x > y > 0 )
Theo bài ra ta có hệ \(\left\{{}\begin{matrix}\left(x+3\right)\left(y+2\right)=xy+45\\\left(x-2\right)\left(y+2\right)=xy\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=39\\2x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=7\end{matrix}\right.\left(tm\right)\)
Diện tích thực là 9 . 7 = 63 m^2

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm

Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.

\(b,\text{PT hoành độ giao điểm: }3x-1=x+2\\ \Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow y=\dfrac{7}{2}\Leftrightarrow A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\\ \text{Vậy }A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\text{ là giao 2 đths}\\ c,\left(D_2\right)\text{//}\left(D\right);B\left(1;0\right)\in\left(D_2\right)\Leftrightarrow\left\{{}\begin{matrix}a+b=0\\a=3;b\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-3\end{matrix}\right.\\ \Leftrightarrow\left(D_2\right):y=3x-3\)

a: \(P=\dfrac{2\sqrt{x}-9-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-x+2\sqrt{x}+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b: Để P<1 thì P-1<0
\(\Leftrightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
hay x<9
Kết hợp ĐKXĐ, ta được: 0<=x<9 và x<>4
c: Để P<1 thì 0<=x<9 và x<>4
mà x là số nguyên
nên \(x\in\left\{0;1;2;3;5;6;7;8\right\}\)

\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...



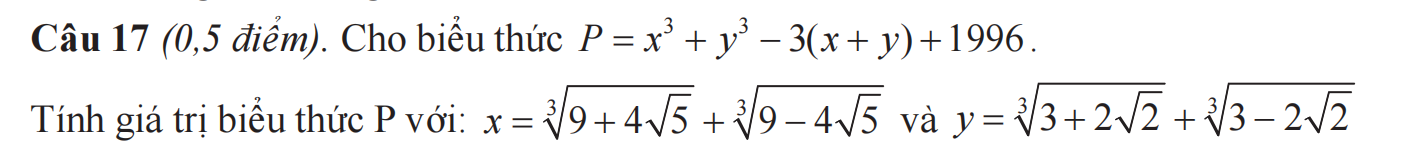 cảm ơn
cảm ơn 


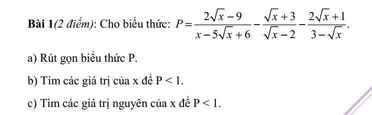

1: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(1)
Ta có: MA=MB
nên M nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
hay OM\(\perp\)AB tại H
Xét ΔOAM vuông tại A có HA là đường cao ứng với cạnh huyền OM
nên \(OA^2=OH\cdot OM\)