
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)



\(a,C=\left(\dfrac{4\sqrt{x}}{2+\sqrt{x}}+\dfrac{8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1}{x-8\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\left(dk:x>0,x\ne4,x\ne64\right)\)
\(=\left(\dfrac{4\sqrt{x}\left(2-\sqrt{x}\right)+8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-8\right)}{\sqrt{x}\left(\sqrt{x}-8\right)}\right)\)
\(=\dfrac{8\sqrt{x}-4x+8x}{4-x}.\dfrac{\sqrt{x}\left(\sqrt{x}-8\right)}{\sqrt{x}-1-2\sqrt{x}+16}\)
\(=\dfrac{8\sqrt{x}+4x}{4-x}.\dfrac{\sqrt{x}\left(\sqrt{x}-8\right)}{-\sqrt{x}+15}\)
\(=\dfrac{4\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-8\right)}{15-\sqrt{x}}\)
\(=\dfrac{4x\left(\sqrt{x}-8\right)}{ \left(2-\sqrt{x}\right)\left(15-\sqrt{x}\right)}\\ =\dfrac{4x\sqrt{x}-32x}{30-2\sqrt{x}-15\sqrt{x}+x}\\ =\dfrac{4x\sqrt{x}-32}{x-17\sqrt{x}+30}\)
\(b,C=-1\Leftrightarrow\dfrac{4x\sqrt{x}-32}{x-17\sqrt{x}+30}=-1\\ \Leftrightarrow4x\sqrt{x}-32+x-17\sqrt{x}+30=0\)
\(\Leftrightarrow4x\sqrt{x}-17\sqrt{x}+x-2=0\\ \Leftrightarrow x=4\left(ktmdk\right)\)
Vậy không có giá trị x thỏa mãn đề bài.

\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.


 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !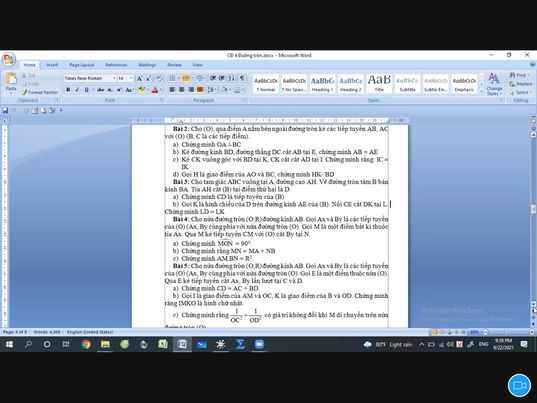

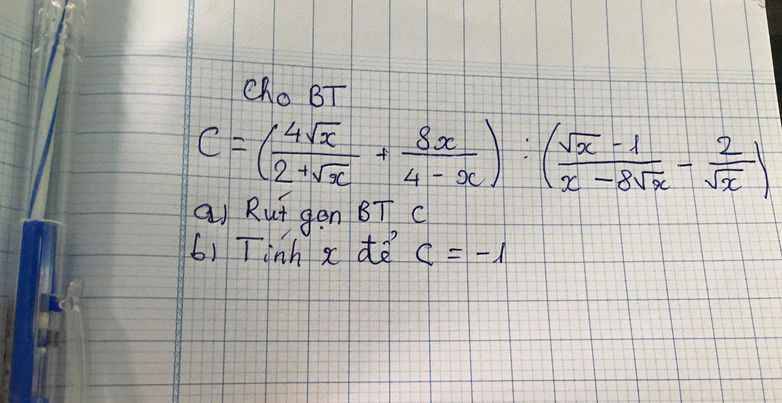

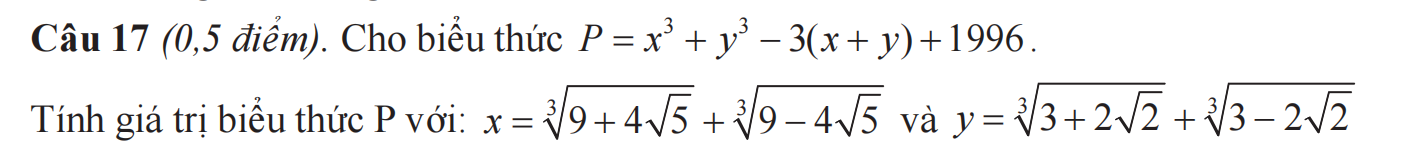 cảm ơn
cảm ơn 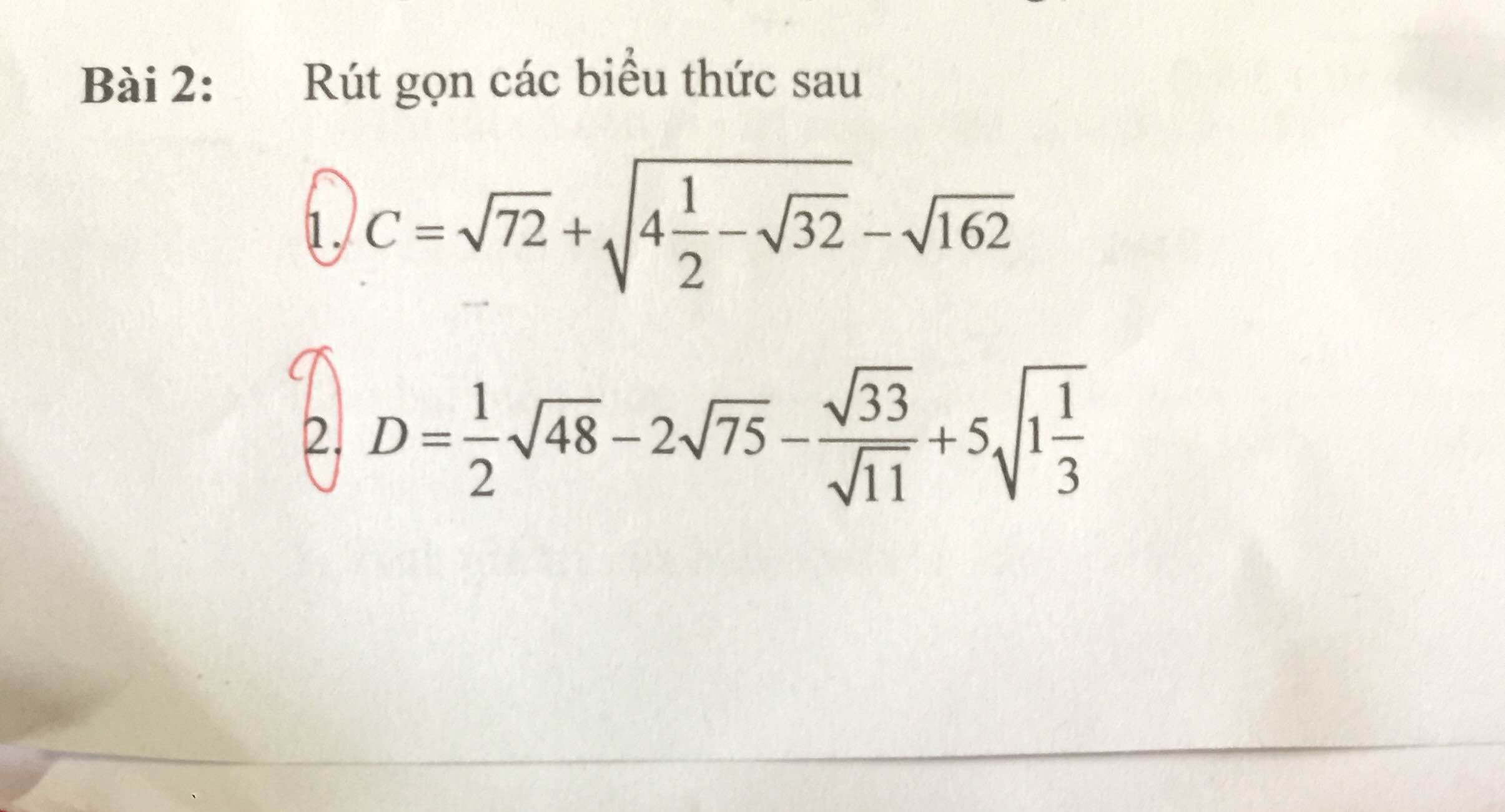
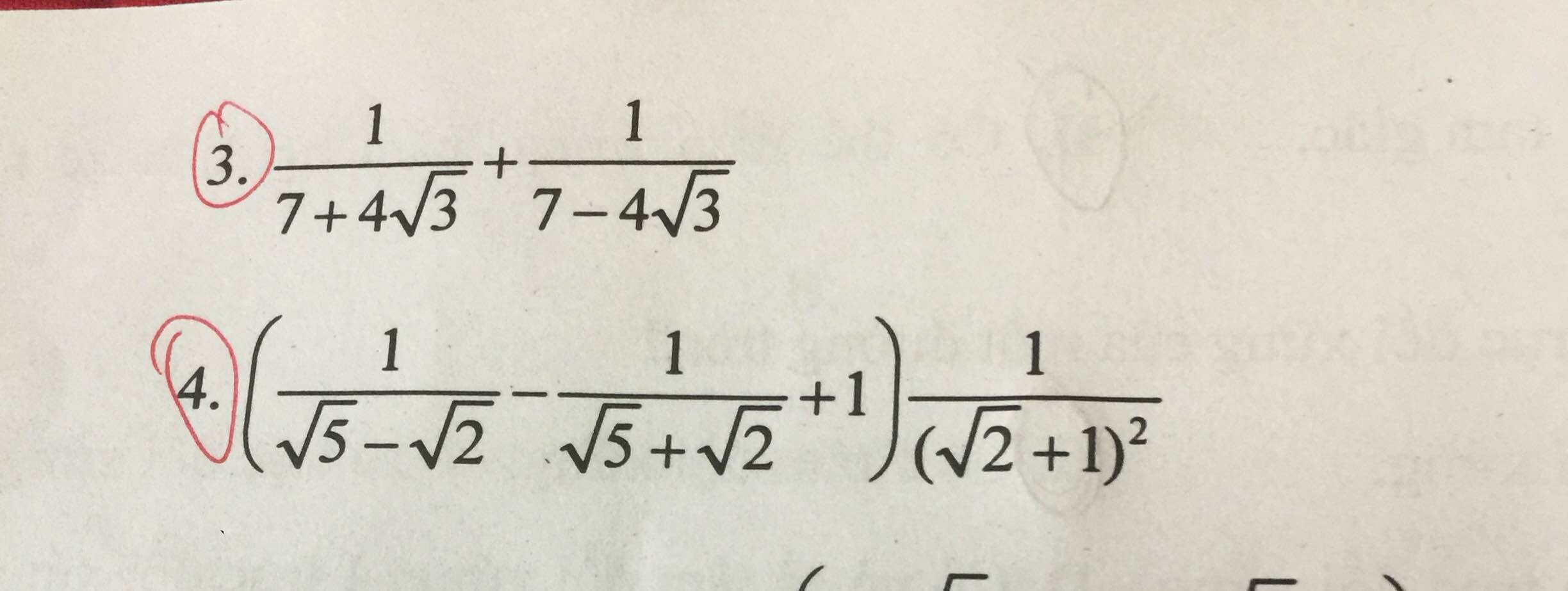

Bạn đăng tách 2 bài ra cho mn cùng giúp nhé
Câu 2:
a: Thay m=-1 vào (1), ta được:
\(x^2-2x+2\cdot\left(-1\right)+3=0\)
=>x=1
b: \(\text{Δ}=\left(2m+4\right)^2-4\left(2m+3\right)=4m^2+16m+16-8m-12\)
\(=4m^2-4m+4=\left(2m-1\right)^2+3>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-1< =0\)
\(\Leftrightarrow\left(2m+4\right)^2-2\left(2m-3\right)-1< =0\)
\(\Leftrightarrow4m^2+16m+16-4m+6-1< =0\)
\(\Leftrightarrow4m^2+12m+21< =0\)
\(\Leftrightarrow m\in\varnothing\)