1: Xét ΔAEB và ΔCED có

EA=EC

EB=ED

AB=CD

=>ΔAEB=ΔCED

2: ΔAEB=ΔCED

=>góc BAE=góc DCE

=>góc BAE=góc CAE

=>AE là phân giác của góc BAC

help

\(a,\frac{13}{x-1}+\frac{5}{2x-2}-\frac{6}{3x-3}=3\)

\(\Leftrightarrow\frac{13}{x-1}+\frac{5}{2\left(x-1\right)}-\frac{6}{3\left(x-1\right)}\)

\(\Leftrightarrow\frac{13.2+5-4}{2\left(x-1\right)}=3\)

\(\Leftrightarrow6\left(x-1\right)=27\)

\(\Leftrightarrow x-1=\frac{9}{2}\Leftrightarrow x=\frac{11}{2}\)

\(b,\frac{2x}{3}-\frac{3}{4}>0\)

\(\Leftrightarrow\frac{8x-9}{12}>0\)

\(\Leftrightarrow8x-9>0\Rightarrow x>\frac{9}{8}\)

\(=\) 4x-2-3x+3=2x+1

\(=\)4x-3x-2x=1+2-3

\(=\)-1x = 0

\(=\)x=0

còn cách khác ko hả bạn

Câu 6.6 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1

Tính M=820+420425+645M=820+420425+645.

Giải

M=820+420425+645=(23)20+(22)20(22)25+(26)5M=820+420425+645=(23)20+(22)20(22)25+(26)5

      =260+240250+230=240(220+1)230(220+1)=210=1024.=260+240250+230=240(220+1)230(220+1)=210=1024.

Câu 6.7 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1

Tìm x, biết:

a) (x4)2=x12x5(x≠0);(x4)2=x12x5(x≠0);

b) x¹⁰ = 25x⁸.

Giải

a) (x4)2=x12x5(x≠0)⇒x8=x7(x4)2=x12x5(x≠0)⇒x8=x7

⇒x8−x7=0⇒x7.(x−1)=0⇒x8−x7=0⇒x7.(x−1)=0

⇒x−1=0⇒x−1=0 (vì x⁷ ≠ 0)

Vậy x = 1.

b) x10=25x8⇒x10−25x8=0⇒x8.(x2−25)=0x10=25x8⇒x10−25x8=0⇒x8.(x2−25)=0

Suy ra x⁸ = 0 hoặc x² - 25 = 0.

Do đó x = 0 hoặc x = 5 hoặc x = -5.

Vậy x∈{0;5;−5}x∈{0;5;−5}.

Câu 6.8 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1

Tìm x, biết:

a) (2x+3)2=9121(2x+3)2=9121;         

b) (3x−1)3=−827(3x−1)3=−827

Giải

a) (2x+3)2=9121=(±311)2(2x+3)2=9121=(±311)2

Nếu 2x+3=311⇒x=−15112x+3=311⇒x=−1511

Nếu 2x+3=−311⇒x=−18112x+3=−311⇒x=−1811

b) (3x−1)3=−827=(−23)3(3x−1)3=−827=(−23)3

⇔3x−1=−23⇔x=19

A= 3/4 +2/5-7/5+5/4

  = (3/4 + 5/4) + (2/5-7/5)

  = 2 + (-1)

  = 1

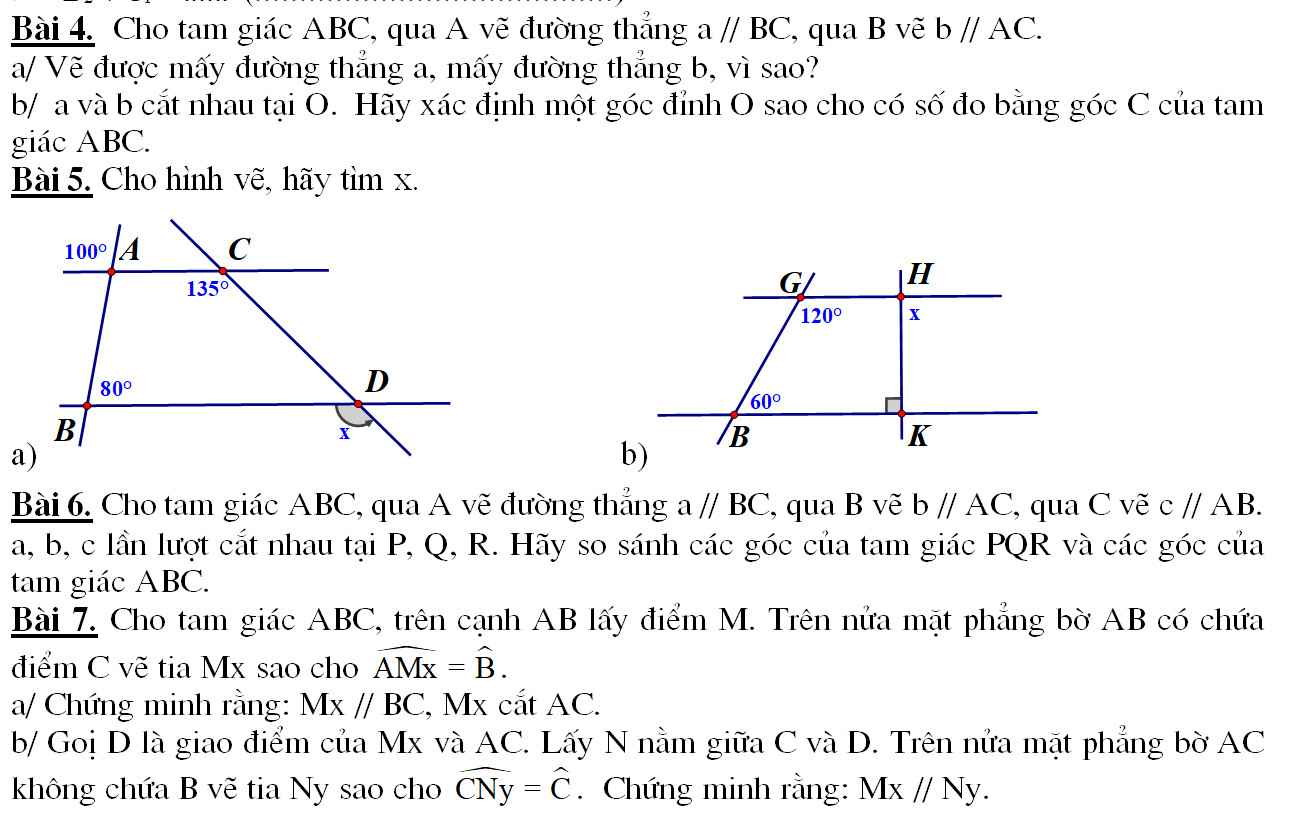
Bài 5:

Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)

            \(100^o+\widehat{A_3}=180^o\)

            \(\widehat{A_3}=80^o\)

Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)

            \(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị 

\(\Rightarrow AC//BD\)

\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)

\(x=135^o\)

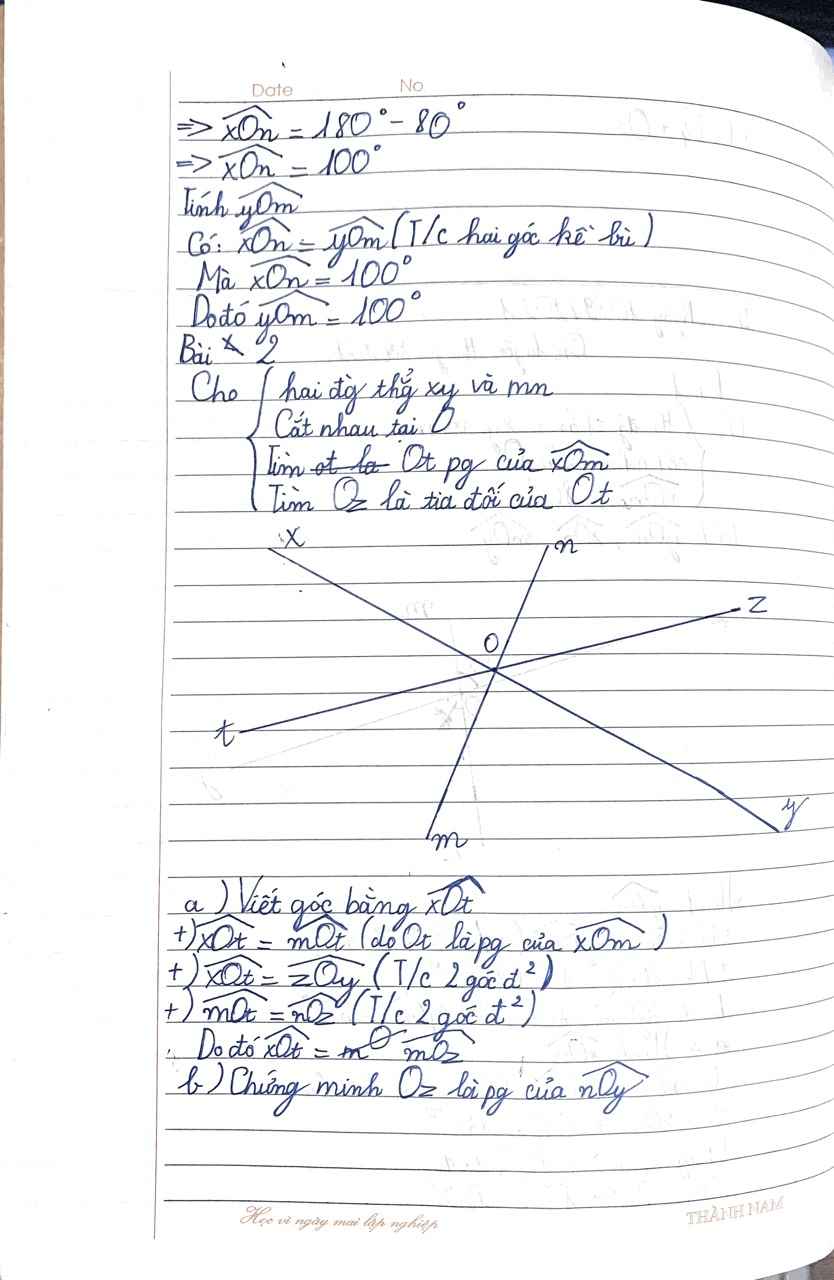
b)

Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)

               \(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía

\(\Rightarrow QH//BK\)

\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)

\(x=90^o\)