
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
a: \(f\left(x\right)=4x^4-x^3-4x^2+x-1\)
\(g\left(x\right)=x^4+4x^3+x-5\)
b: \(f\left(x\right)-g\left(x\right)=4x^4-x^3-4x^2+x-1-x^4-4x^3-x+5\)
\(=3x^4-5x^3-4x^2+4\)
\(f\left(x\right)+g\left(x\right)=4x^4-x^3-4x^2+x-1+x^4+4x^3+x-5\)
\(=5x^4+3x^3-4x^2+2x-6\)

\(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.5^44^4}{5^4.5.5^4.5.4^4.4}=\dfrac{5^8.4^4}{5^4.5^4.5.5.4^4.4.4.}=\dfrac{5^8.4^4}{5^8.5^2.4^4.4}\)\(=\dfrac{1}{5^2.4}=\dfrac{1}{100}=0,01\)
c)
\(\dfrac{5^4.20^4}{25^5.4^5}\)
\(=\dfrac{5^4.\left(5.4\right)^4}{\left(5^2\right)^5.\left(2^2\right)^5}\)
\(=\dfrac{5^4.5^4.4^4}{5^{10}.2^{10}}\)
\(=\dfrac{5^8.\left(2^2\right)^4}{5^{10}.2^{10}}\)
\(=\dfrac{5^8.2^8}{5^{10}.2^{10}}\)
\(=\dfrac{1}{5^2.2^2}\)
\(=\dfrac{1}{25.4}\)
\(=\dfrac{1}{100}\)

Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM

a) Ta có: \(y=f\left(x\right)=4x^2-5\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(3\right)=4.3^2-5=31\\f\left(-\dfrac{1}{2}\right)=4.\left(-\dfrac{1}{2}\right)^2-5=-4\end{matrix}\right.\)
b) Ta có: \(f\left(x\right)=-1\)
\(\Rightarrow4x^2-5=-1\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\) thì \(f\left(x\right)=-1\)
c) \(\forall x\in R,f\left(x\right)=f\left(-x\right)\Leftrightarrow f\left(-x\right)=4.\left(-x\right)^2-5=4x^2-5=f\left(x\right)\)
Vậy \(\forall x\in R\) thì \(f\left(x\right)=f\left(-x\right)\)
\(a.f\left(3\right)=4.3^2-5=31.\\ f\left(\dfrac{-1}{2}\right)=4.\left(\dfrac{-1}{2}\right)^2-5=-4.\)
\(b.f\left(x\right)=-1.\Rightarrow4x^2-5=-1.\\ \Leftrightarrow4x^2=4.\Leftrightarrow x^2=1.\\ \Leftrightarrow x=\pm1.\)
\(c.f\left(x\right)=f\left(-x\right).\\ \Rightarrow4x^2-5=4\left(-x\right)^2-5.\\ \Leftrightarrow4x^2-5=4x^2-5.\)
\(\Leftrightarrow0x=0\) (luôn đúng).
Vậy với mọi x ∈ R thì f (x)= f (-x).
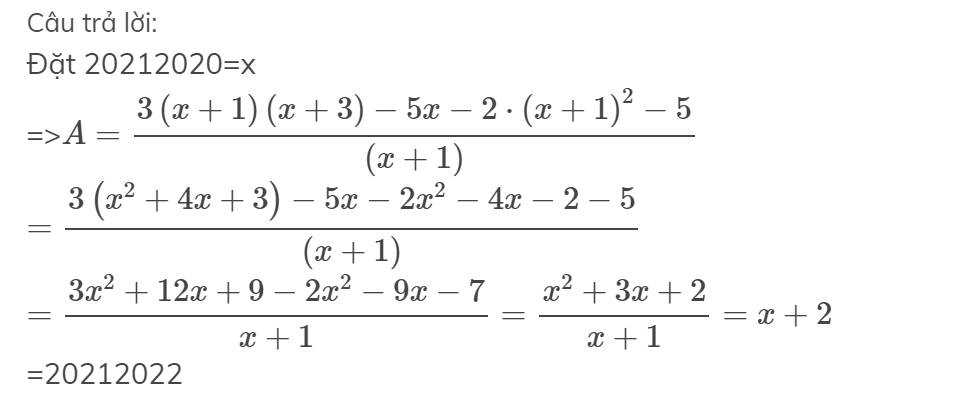





Đặt 20212020=x
=>\(A=\dfrac{3\left(x+1\right)\left(x+3\right)-5x-2\cdot\left(x+1\right)^2-5}{\left(x+1\right)}\)
\(=\dfrac{3\left(x^2+4x+3\right)-5x-2x^2-4x-2-5}{\left(x+1\right)}\)
\(=\dfrac{3x^2+12x+9-2x^2-9x-7}{x+1}=\dfrac{x^2+3x+2}{x+1}=x+2\)
=20212022