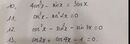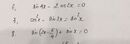giải hình nào cx đc nha ko cần giải hết đâu
ai giải hết thì tym sập nhà 

ai giải 1 ảnh thì tym 3tus

Chia nhỏ ra, gửi từng hình 1 thôi em

Nhiều quá kéo chuột đã thấy mòn con chuột rồi

a: Tọa độ M' là:

\(\left\{{}\begin{matrix}x=2+1=3\\y=-1-3=-4\end{matrix}\right.\)

Lấy A(-1;1) thuộc (d)

=>A'(0;-2)

Thay x=0 và y=-2 vào (d'): 2x-3y+c=0, ta được:

c+2*0-3*(-2)=0

=>c=-6

b: Tọa độ M' là:

\(\left\{{}\begin{matrix}x=2\cdot cos\left(-90\right)-\left(-1\right)\cdot sin\left(-90\right)=-1\\y=2\cdot sin\left(-90\right)+\left(-1\right)\cdot cos\left(-90\right)=-2\end{matrix}\right.\)

A(-1;1)

Tọa độ A' là: 

\(\left\{{}\begin{matrix}x=-1\cdot cos\left(-90\right)-1\cdot sin\left(-90\right)=1\\y=-1\cdot sin\left(-90\right)+1\cdot cos\left(-90\right)=1\end{matrix}\right.\)

Thay x=1 và y=1 vào 3x+2y+c=0, ta được:

c+3+2=0

=>c=-5

đến đó chắc tự giải tiếp đc nhỉ

Bạn ơi, xem lại giúp mình nhé ở dòng thứ 3 đang là -4sinxcosx sao xuống dưới lại là -8sinxcosx được. Cảm ơn vì đã giúp mình nhé :>

\(\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x+2\cos^2x-1\right)-\sin2x-\cos x=0\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x+2\cos^2x-1-2\cos^2x+1-\cos x\right)=0\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x-\cos x\right)=0\Rightarrow\left[{}\begin{matrix}2\sin x+1=0\\\sqrt{3}\sin x-\cos x=0\end{matrix}\right.\)

\(a=\lim\limits_{x\rightarrow-3}\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}=\lim\limits_{x\rightarrow-3}\dfrac{1}{x-3}=-\dfrac{1}{6}\)

\(b=\lim\limits_{x\rightarrow2}\dfrac{\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+3}{x+2}=\dfrac{5}{4}\)

\(c=\lim\limits_{x\rightarrow4}\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x+5\right)\left(x-4\right)}=\lim\limits_{x\rightarrow4}\dfrac{x+4}{x+5}=\dfrac{8}{9}\)

\(d=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+2}{x-1}=4\)

\(e=\lim\limits_{x\rightarrow2}\dfrac{x+7-9}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{\sqrt{x+7}+3}=\dfrac{1}{6}\)

\(f=\lim\limits_{x\rightarrow1}\dfrac{x+3-4}{\left(x-1\right)\left(\sqrt{x+3}+2\right)}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt{x+3}+2\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt{x+3}+2}=\dfrac{1}{4}\)

\(h=\lim\limits_{x\rightarrow-3}\dfrac{x+7-4}{\left(x+3\right)\left(\sqrt{x+7}+2\right)}=\lim\limits_{x\rightarrow-3}\dfrac{x+3}{\left(x+3\right)\left(\sqrt{x+7}+2\right)}=\lim\limits_{x\rightarrow-3}\dfrac{1}{\sqrt{x+7}+2}=\dfrac{1}{4}\)

Bài 1:

a, 

= lim_x->-3 \(\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}\)

= lim_x->3  x-3

= -3 -3

= -6

b, 

= lim_x->2 \(\dfrac{\left(x-2\right)\left(x+3\right)}{\left(x-2\right)\left(x+2\right)}\)

= lim_x->2  \(\dfrac{x+3}{x+2}\)

= \(\dfrac{5}{4}\)

c,

= lim_x->4   \(\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)\left(x+5\right)}\)

= lim_x->4   \(\dfrac{\left(x+4\right)}{\left(x+5\right)}\)

= \(\dfrac{8}{9}\)

d,

= lim_x->2   \(\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x-1\right)}\)

= lim_x->2   \(\dfrac{\left(x+2\right)}{\left(x-1\right)}\)

= 4