
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{2^{12}\cdot3^5-4^6\cdot9^2}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}-\dfrac{5^{10}\cdot7^3-25^5\cdot49^2}{\left(125\cdot7\right)^3+5^9\cdot14^3}\)
\(A=\dfrac{2^{12}\cdot3^5-2^{12}\cdot3^4}{2^{12}\cdot3^6+2^{12}\cdot3^5}-\dfrac{5^{10}\cdot7^3-5^{10}\cdot7^4}{125^3\cdot7^3+5^9\cdot14^3}\)
\(A=\dfrac{2^{12}\left(3^5-3^4\right)}{2^{12}\left(3^6+3^5\right)}-\dfrac{5^{10}\cdot7^3-5^{10}\cdot7^4}{5^9\cdot7^3+5^9\cdot14^3}\)
\(A=\dfrac{2^{12}\left(3^5-3^4\right)}{2^{12}\left(3^6+3^5\right)}-\dfrac{5^{10}\left(7^3-7^4\right)}{5^9\left(7^3+14^3\right)}\)
\(A=\dfrac{162}{972}-\dfrac{5\left(-2058\right)}{3087}\)
\(A=\dfrac{1}{6}-\left(-\dfrac{10}{3}\right)\)
\(A=\dfrac{7}{2}\)

a: AC^2=AB^2+BC^2
=>ΔBAC vuông tại B
b: Xét ΔEAD có
EB vừa là đường cao, vừa là trung tuyến
=>ΔEAD cân tại E
c: Xét ΔCAD có
CB là trung tuyến
CE=2/3CB
=>E là trọng tâm
=>K,A,E thẳng hàng
d: (BA+BC)^2=BA^2+BC^2+2*BA*BC
=CA^2+2*BH*AC<CA^2+2*BH*AC+BH^2=(CA+BH)^2
=>BA+BC<CA+BH

mình mới học lớp 5 thôi,phần đầu hiểu phần đầu còn phần phần cuối thì.......không hiểu!?

\(c,=4\cdot\left(-\dfrac{1}{8}\right)-2\cdot\dfrac{1}{4}-\dfrac{3}{2}+1=-\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{3}{2}+1=-\dfrac{3}{2}\\ \left(5x+\dfrac{2}{3}\right)^2=\dfrac{1}{4}\Rightarrow\left[{}\begin{matrix}5x+\dfrac{2}{3}=\dfrac{1}{2}\\5x+\dfrac{2}{3}=-\dfrac{1}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}5x=-\dfrac{1}{6}\\5x=-\dfrac{7}{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{30}\\x=-\dfrac{7}{30}\end{matrix}\right.\\ c,x:2=\left(-4\right):5\Rightarrow x=-\dfrac{4}{5}\cdot2=-\dfrac{8}{5}\)

a: Xét ΔABI và ΔAEI có
AB=AE
\(\widehat{BAI}=\widehat{EAI}\)
AI chung
Do đó: ΔABI=ΔAEI
b: Xét ΔABE có AB=AE
nên ΔABE cân tại A
mà AF là đường phân giác
nên AF là đường cao
c: \(\widehat{ABE}=\dfrac{180^0-80^0}{2}=50^0\)

a: Thay x=-2 vào A, ta được:
\(A=\dfrac{1}{4}\left(-2\right)^4+\dfrac{1}{2}\cdot\left(-2\right)^2-5\)
\(=\dfrac{1}{4}\cdot16+\dfrac{1}{2}\cdot4-5\)
=4+2-5
=1
b: \(A=\dfrac{1}{4}x^4+\dfrac{1}{2}x^2-5\)
\(=\left(\dfrac{1}{2}x^2\right)^2+2\cdot\dfrac{1}{2}x^2\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{21}{4}\)
\(=\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)^2-\dfrac{21}{4}\)
ta có: \(\dfrac{1}{2}x^2>=0\forall x\)
=>\(\dfrac{1}{2}x^2+\dfrac{1}{2}>=\dfrac{1}{2}\forall x\)
=>\(\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)^2>=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\forall x\)
=>\(A=\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)^2-\dfrac{21}{4}>=\dfrac{1}{4}-\dfrac{21}{4}=-5\forall x\)
Dấu '=' xảy ra khi x=0

a: =>|x-2,5|=0,75
=>x-2,5=0,75 hoặc x-2,5=-0,75
=>x=3,25 hoặc x=1,75
b: =>|1,25-2x|=1/2-1/3=1/6
=>5/4-2x=1/6 hoặc 5/4-2x=-1/6
=>x=13/24 hoặc x=17/24
c: =>|2x-1|=|x+1/3|
=>2x-1=x+1/3 hoặc 2x-1=-x-1/3
=>x=4/3 hoặc 3x=2/3
=>x=2/9 hoặc x=4/3
d: =>x>=-1 và (2x+15)^2=(x-1)^2
=>(2x+15-x+1)(2x+15+x-1)=0 và x>=-1
=>(x+16)(3x+14)=0
=>x thuộc rỗng

4^2.4^3/2^10=(2^2)^2/(2^2)^10=2^4/2^20=1/2^16
Nho cho minh nhe
Yen tam minh hoc roi khong sai dau


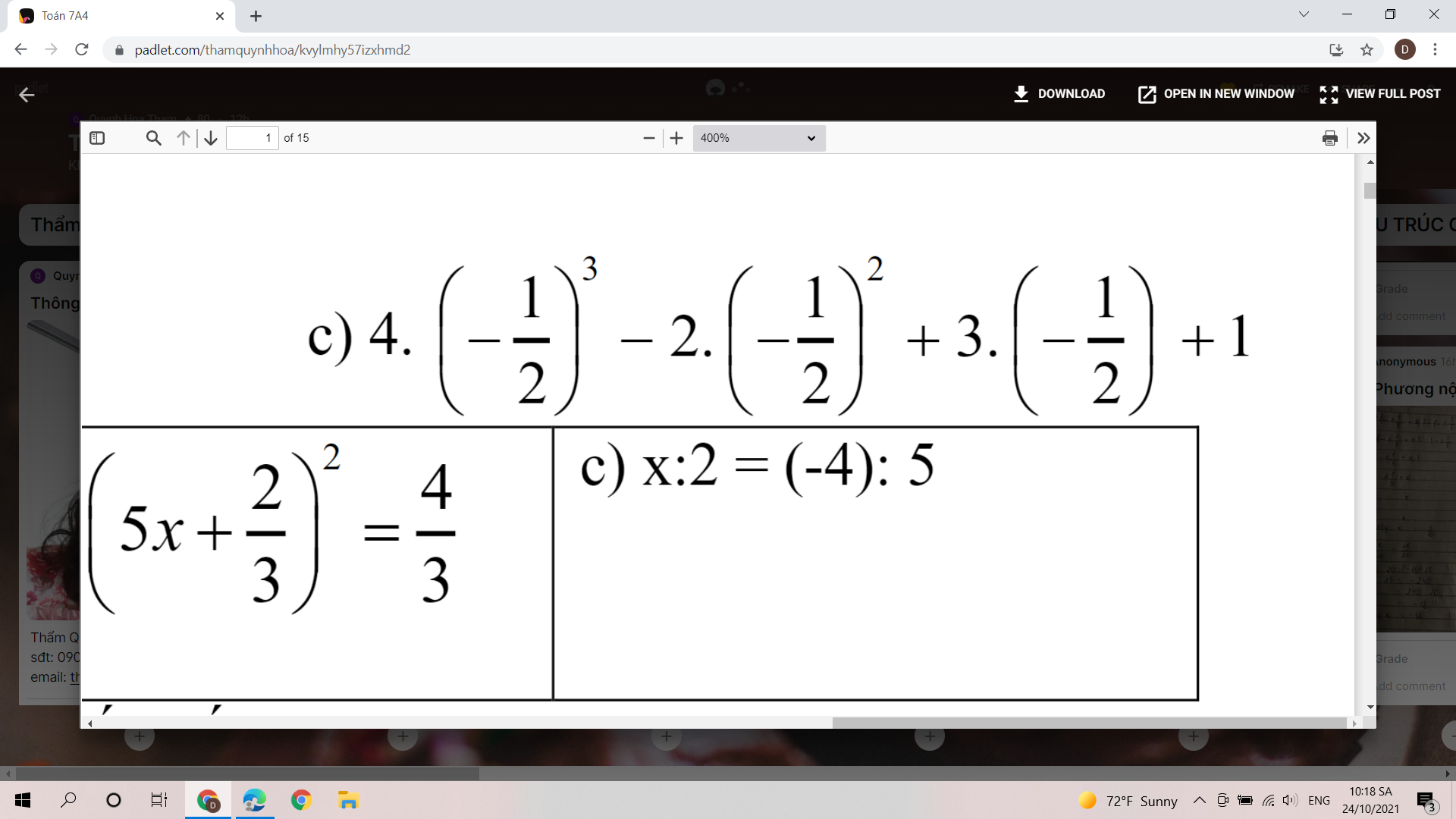
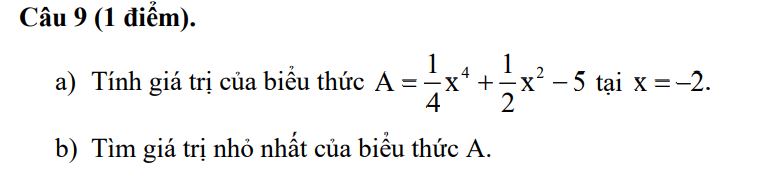

Bài 5 :
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=k\Rightarrow a=2k;b=3k\)
Thay vào ta được
\(Q=\dfrac{2.4k^2+5.9k^2}{6.4k^2-5.9k^2}=\dfrac{53k^2}{-21k^2}=-\dfrac{53}{21}\)
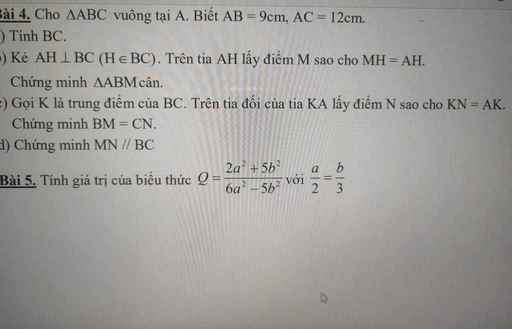
a:BC=15cm
b: Xét ΔABM có
BH là đườg cao
BH là đường trung tuyến
Do đó:ΔABM cân tại B
c: Xét tứ giác ABNC có
K là trung điểm của AN
K là trung điểm của BC
Do đó: ABNC là hình bình hành
Suy ra: CN=AB
mà AB=BM
nên CN=BM
d: Xét ΔAMN có
H là trung điểm của AM
K là trung điểm của AN
DO đó: HK là đường trung bình
=>HK//NM
hay NM//BC