Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

202³⁰³ = (202³)¹⁰¹ = 8242408¹⁰¹
303²⁰² = (303²)¹⁰¹ = 91809¹⁰¹
Do 8242408 > 91809 nên 8282408¹⁰¹ > 91809¹⁰¹
Vậy 202³⁰³ > 303²⁰²

Cho hình chữ nhật ABCD có M, N nằm trên cạnh AD và cho ÂM = MN = ND = 3cm.
a) So sánh diện tích tam giác BMN và BNC
b) So sánh diện tích tam giác MNB và CNM
c) So sánh diện tích tam giác ABM và MBN
d) So sánh diện tích hình thang AMCB và ABCD
Gợi ý:
Bạn vẽ hình ra
Nhìn vào hình vẽ suy luận ra các mối liên hệ
Vận dụng Các kiến thức đã học để làm bài
Nhớ lại những gì thầy cô giảng
Thế là bạn sẽ làm được thui

a: \(5^{300}=25^{150}\)
\(3^{450}=27^{150}\)
mà 25<27
nên \(5^{300}< 3^{450}\)
a: 5300=251505300=25150
3450=271503450=27150
mà 25<27
nên 5300<3450

nếu a>0
thì 5a>0
(-5)a<0
nếu a=0 thì
5a=0
(-5)a=0
nếu a<0 thì
5a<0
(-5)a>0
bạn kích vào chữ đúng dưới mỗi câu trả lời. đó là cách k đúng.
lưu ý: ĐỪNG KÍCH CHỮ SAI

Ta xét : \(B=\left(2017\right).2019=\left(2018-1\right)\left(2018+1\right)\)
\(B=2018.2018+2018-2018-1\)
\(B=2018.2018-1\)
Mà : \(A=2018.2018\)
\(Dođó:A>B\)

Giải:
a)Ta có:
C=1957/2007=1957+50-50/2007
=2007-50/2007
=2007/2007-50/2007
=1-50/2007
D=1935/1985=1935+50-50/1985
=1985-50/1985
=1985/1985-50/1985
=1-50/1985
Vì 50/2007<50/1985 nên -50/2007>-50/1985
⇒C>D
b)Ta có:
A=20162016+2/20162016-1
A=20162016-1+3/20162016-1
A=20162016-1/20162016-1+3/20162016-1
A=1+3/20162016-1
Tương tự: B=20162016/20162016-3
B=1+3/20162016-3
Vì 20162016-1>20162016-3 nên 3/20162016-1<3/20162016-3
⇒A<B
Chúc bạn học tốt!
Làm tiếp:
c)Ta có:
M=102018+1/102019+1
10M=10.(102018+1)/202019+1
10M=102019+10/102019+1
10M=102019+1+9/102019+1
10M=102019+1/102019+1 + 9/102019+1
10M=1+9/102019+1
Tương tự:
N=102019+1/102020+1
10N=1+9/102020+1
Vì 9/102019+1>9/102020+1 nên 10M>10N
⇒M>N
Chúc bạn học tốt!

a,\(A=\frac{1}{5}+\frac{1}{5^2}+\frac{1}{5^3}+...+\frac{1}{5^{100}}\)
\(=>5A=1+\frac{1}{5}+\frac{1}{5^2}+...+\frac{1}{5^{99}}\)
\(=>5A-A=1-\frac{1}{5^{100}}=>A=\frac{1-\frac{1}{5^{100}}}{4}\)
b, Ta có \(1-\frac{1}{5^{100}}< 1=>\frac{1-\frac{1}{5^{100}}}{4}< \frac{1}{4}\)hay \(A< \frac{1}{4}\)
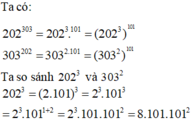
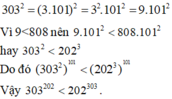
b: Đặt 101=a
=>\(202^{303}=\left(2a\right)^{3a}=\left(8a^3\right)^a\) và \(303^{202}=\left(3a\right)^{2a}=\left(9a^2\right)^a\)
\(8a^3-9a^2=a^2\left(8a-9\right)\)
\(=101^2\cdot\left(8\cdot101-9\right)=101^2\cdot799>0\)
=>\(8a^3>9a^2\)
=>\(\left(8a^3\right)^a>\left(9a^2\right)^a\)
=>\(202^{303}>303^{202}\)
c: Đặt 111=a
=>\(222^{777}=\left(2a\right)^{7a}=\left[\left(2a\right)^7\right]^a=\left(128a^7\right)^a\) và \(777^{222}=\left(7a\right)^{2a}=\left(49a^2\right)^a\)
mà \(128a^7>49a^2\)
nên \(222^{777}>777^{222}\)
oki