
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(C=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{601}-\dfrac{1}{604}=1-\dfrac{1}{604}=\dfrac{603}{604}\)

B2"
`a)3/4+1/2-1/4`
`=3/4-1/4+1/2`
`=1/2+1/2=1`
`b)(-2)/3*5/7+(-2)/3*2/7+5/3`
`=(-2)/3*(5/7+2/7)+5/3`
`=-2/3+5/3=1`
`c)(-5)/9+5/9:(1 2/3-2 1/6)`
`=(-5)/9+5/9:(5/3-13/6)`
`=(-5)/9+5/9:(-3)/6`
`=(-5)/9+5/9*(-2)`
`=5/9*(-1-2)`
`=5/9*(-3)=-5/3`
b3:
`a)x*3/6=2/3`
`=>x*1/2=2/3`
`=>x=4/3`
`b)x/150=5/6*(-7)/25`
`=>x/150=(-7)/(6*5)=-7/30`
`=>x/150=(-35)/150`
`=>x=-35`
`c)1/2x+3/5x=3`
`=>11/10x=3`
`=>x=3*10/11=30/11`


a: Bạn chụp rõ đề lại nha
b: \(9A=\dfrac{3^{125}+9}{3^{125}+1}=1+\dfrac{8}{3^{125}+1}\)
\(9B=\dfrac{3^{124}+1-1}{3^{124}+1}=1-\dfrac{1}{3^{124}+1}\)
mà 8/3^125+1>0>-1/3^124+1
nên 9A>9B
=>A>B

\(=\left(\dfrac{1}{49}-\dfrac{1}{9}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49^2}\right)=0\)


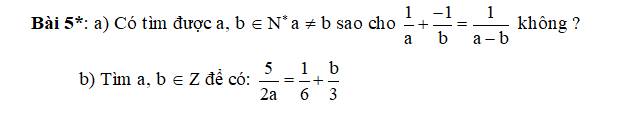 Giúp mình với . Cảm ơn rất nhiều !
Giúp mình với . Cảm ơn rất nhiều !

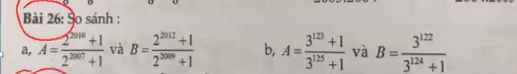
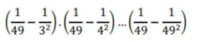



Lời giải:
a.
$\frac{1}{a}+\frac{-1}{b}=\frac{1}{a-b}$
$\Rightarrow \frac{b-a}{ab}=\frac{1}{a-b}$
$\Rightarrow (b-a)(a-b)=ab$
$\Rightarrow -(a-b)^2=ab$
Với $a,b\in\mathbb{N}^*$, $ab>0$ còn $-(a-b)^2\leq 0$
Do đó $-(a-b)^2\neq ab$
$\Rightarrow$ không tồn tại $a,b\in\mathbb{N}^*$ thỏa mãn điều kiện đề.
b.
$\frac{5}{2a}=\frac{1}{6}+\frac{b}{3}$
$\frac{15}{6a}=\frac{1+2b}{6}=\frac{a+2ab}{6a}$
$\Rightarrow a+2ab=15$
$\Rightarrow a(1+2b)=15$
Do $a,b$ nguyên nên $a, 1+2b$ nguyên. Mà tích $a(1+2b)=15$ nên xét các TH sau:
TH1: $a=1, 2b+1=15\Rightarrow a=1; b=7$
TH2: $a=-1, 2b+1=-15\Rightarrow a=-1; b=-8$
TH3: $a=15, 2b+1=1\Rightarrow a=15; b=0$
TH4: $a=-15; 2b+1=-1\Rightarrow a=-15; b=-1$
TH5: $a=3, 2b+1=5\Rightarrow a=3; b=2$
TH6: $a=-3, 2b+1=-5\Rightarrow a=-3; b=-3$
TH7: $a=5; 2b+1=3\Rightarrow a=5; b=1$
TH8: $a=-5; 2b+1=-3\Rightarrow a=-5; b=-2$
e cảm ơn