Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
1: Ta có: \(A=3\sqrt{25}-\sqrt{36}-\sqrt{64}\)
\(=3\cdot5-6-8\)
\(=15-6-8=1\)
Câu I:
2: Ta có: \(B=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{x+1}{x-1}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{x+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-\sqrt{x}+x+\sqrt{x}-x-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-1}{x-1}=1\)

Em tách ra 1-2 bài/1 câu hỏi để mọi người hỗ trợ nhanh nhất nha!

\(A=\dfrac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\)
\(=2\sqrt{y}\)
\(B=\dfrac{x+y-2\sqrt{xy}}{\sqrt{x}-\sqrt{y}}-\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\left(\sqrt{x}-\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\)
\(=0\)
\(C=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}+\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{x}\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}=\sqrt{x}+\sqrt{y}+\sqrt{x}+\sqrt{y}\)
\(=2\left(\sqrt{x}+\sqrt{y}\right)\)
\(D=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-4\sqrt{xy}}{\sqrt{x}-\sqrt{y}}+\dfrac{y\sqrt{x}-x\sqrt{y}}{\sqrt{xy}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{y}-\sqrt{x}\right)}{\sqrt{xy}}=\sqrt{x}-\sqrt{y}+\sqrt{y}-\sqrt{x}=0\)

\(7,\\ a,ĐK:a>0;a\ne1\\ b,K=\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ K=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}=\dfrac{a-1}{\sqrt{a}}\\ c,a=3+2\sqrt{2}=\left(\sqrt{2}+1\right)^2\\ \Leftrightarrow K=\dfrac{3+2\sqrt{2}-1}{\sqrt{2}+1}=\dfrac{2+2\sqrt{2}}{\sqrt{2}+1}=\dfrac{2\left(\sqrt{2}+1\right)}{\sqrt{2}+1}=2\\ d,K< 0\Leftrightarrow a-1< 0\left(\sqrt{a}>0\right)\Leftrightarrow0< a< 1\)

\(\left(\sqrt{5-2\sqrt{6}}+\sqrt{2}\right)\cdot\dfrac{1}{\sqrt{3}}\)
\(=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}\)
=1







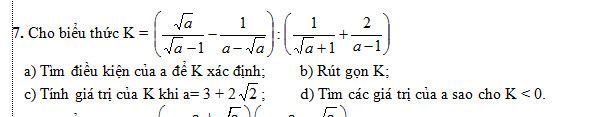


1:
ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BC=\dfrac{9^2}{5.4}=15\left(cm\right)\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
BC=BH+CH
=>CH=BC-BH=15-5,4=9,6cm
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot15=9\cdot12=108\)
=>AH=7,2(cm)
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF=7,2(cm)
Xét ΔABC vuông tại A có
\(sinABC=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{ABC}\simeq53^0\)
=>\(\widehat{HAC}=\widehat{ABC}\simeq53^0\)
2:
ΔHAB vuông tại H có HE là đường cao
nên \(HE\cdot BA=HA\cdot HB\)
=>\(HE\cdot9=5.4\cdot7.2\)
=>\(HE=5.4\cdot0.8=4.32\left(cm\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(HF\cdot AC=HA\cdot HC\)
=>\(HF\cdot12=9.6\cdot7.2\)
=>\(HF=0.8\cdot7.2=5.76\left(cm\right)\)
\(S_{AEHF}=HE\cdot HF=5.76\cdot4.32=24.8832\left(cm^2\right)\)
\(S_{AEF}=\dfrac{1}{2}\cdot AE\cdot AF=\dfrac{1}{2}\cdot5.76\cdot4.32=12.4416\left(cm^2\right)\)
3: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có FH là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
4: \(AB\cdot cosB+AC\cdot cosC\)
\(=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=\dfrac{BC^2}{BC}=BC\)
6:
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật