
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=7\left(1+7+7^2\right)+...+7^{118}\left(1+7+7^2\right)\)
\(=57\left(1+...+7^{118}\right)⋮57\)

3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2


Ta có: \(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{99\cdot100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{2}-\dfrac{1}{100}=\dfrac{50}{100}-\dfrac{1}{100}=\dfrac{49}{100}\)
\(A=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)
\(A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A=\dfrac{1}{2}-\left(\dfrac{1}{3}-\dfrac{1}{3}\right)-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)-\left(\dfrac{1}{5}-\dfrac{1}{5}\right)-...-\left(\dfrac{1}{99}-\dfrac{1}{99}\right)-\dfrac{1}{100}\)
\(A=\dfrac{1}{2}-0-0-0-...-0-\dfrac{1}{100}\)
\(A=\dfrac{1}{2}-\dfrac{1}{100}\)
\(A=\dfrac{50}{100}-\dfrac{1}{100}\)
\(A=\dfrac{49}{100}\)

c: Trường hợp 1: n=2k
\(\Leftrightarrow n\left(n+2017\right)=2k\left(2k+2017\right)⋮2\)
Trường hợp 2: n=2k+1
\(\Leftrightarrow n\left(n+2017\right)=\left(2k+1\right)\left(2k+2018\right)⋮2\)

2S = 2 + 2^2 + 2^3 + ...+ 2^64
2S + 1 = 1 + 2 + 2^2 + ... + 2^64
2S - S = 2^64 - 1
Vậy S = 2^64 - 1
\(A=2^2+2^3+...+2^{62}+2^{63}\)
\(2A=2^3+2^4+...+2^{63}+2^{64}\)
\(2A-A=\left(2^3+2^4+...+2^{63}+2^{64}\right)-\left(2^2+2^3+...+2^{62}+2^{63}\right)\)
\(A=2^{64}-2^2\)

\(a,\Rightarrow20\cdot2^x=160+1-1\\ \Rightarrow2^x=160:20=8=2^3\\ \Rightarrow x=3\\ b,\Rightarrow\left(4-x:2\right)^3=2\left(8-5\right)+1+1\\ \Rightarrow\left(4-x:2\right)^3=6+2=8=2^3\\ \Rightarrow4-x:2=2\\ \Rightarrow x:2=2\Rightarrow x=4\\ c,n\left(n+2017\right)\)
Với n chẵn thì \(n=2k\left(k\in N\right)\Rightarrow n\left(n+2017\right)=2k\left(n+2017\right)⋮2\)
Với n lẻ thì \(n=2k+1\left(k\in N\right)\Rightarrow n\left(n+2017\right)=n\left(2k+2018\right)=2n\left(k+1009\right)⋮2\)
Vậy \(n\left(n+2017\right)\) luôn chẵn
\(d,3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}=\left(2^3\right)^{100}=2^{300}\)
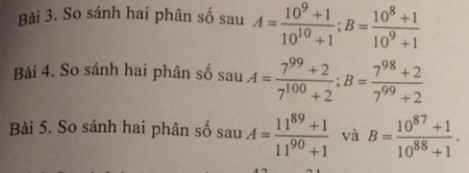
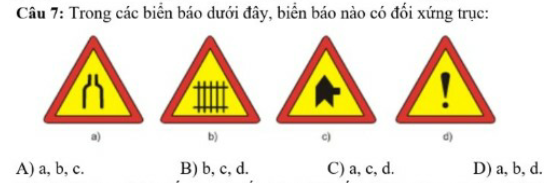


 help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với
help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với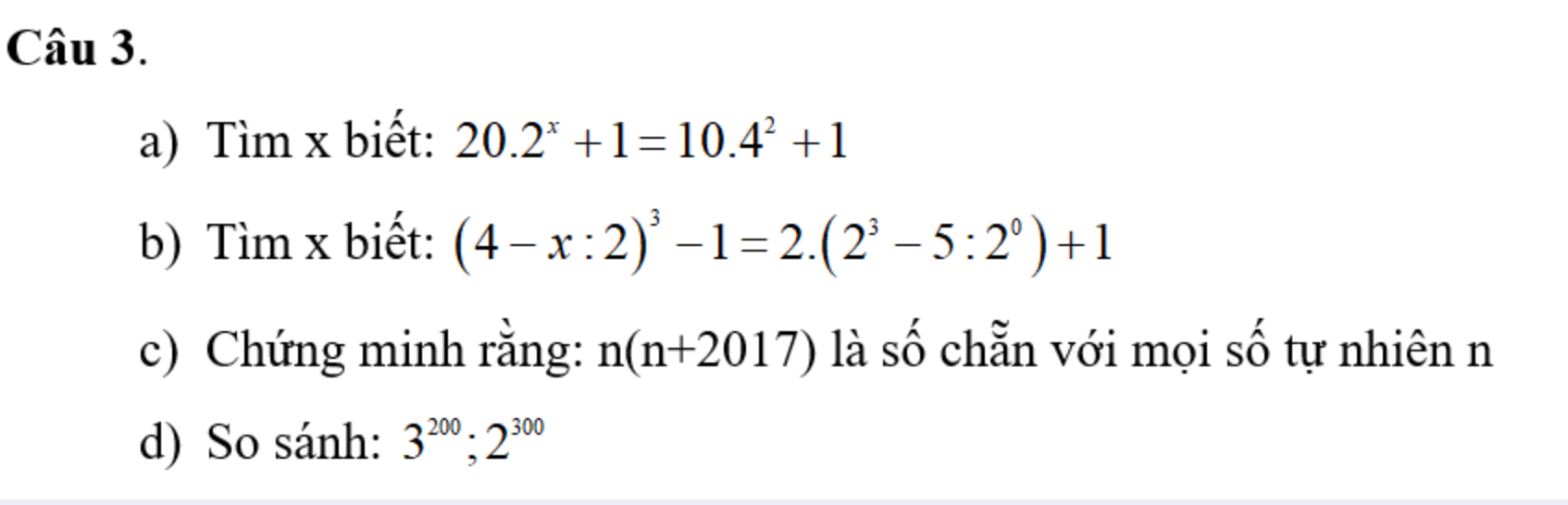 giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
Bài 3:
\(A=\dfrac{10^9+1}{10^{10}+1}\Rightarrow10A=\dfrac{10^{10}+10}{10^{10}+1}\Rightarrow10A-1=\dfrac{9}{10^{10}+1}\)
\(B=\dfrac{10^8+1}{10^9+1}\Rightarrow10B=\dfrac{10^9+10}{10^9+1}\Rightarrow10B-1=\dfrac{9}{10^9+1}\)
\(Do\) \(\dfrac{9}{10^{10}+1}< \dfrac{9}{10^9+1}\Rightarrow10A-1< 10B-1\Rightarrow10A< 10B\Rightarrow A< B\)