
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)

1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3

Lời giải:
$=11(\frac{13}{161}+\frac{4}{203}-\frac{7}{413}):[5(\frac{13}{69}+\frac{4}{87}-\frac{7}{177})]$
$=11.\frac{3}{7}(\frac{13}{69}+\frac{4}{87}-\frac{7}{177}):[5(\frac{13}{69}+\frac{4}{87}-\frac{7}{177})]$
$=11.\frac{3}{7}:5=\frac{33}{35}$


tham khảo tại:https://hoc24.vn/hoi-dap/tim-kiem?q=Cho+%C4%91a+th%E1%BB%A9c+f+(x)+=+ax3+bx2+cx+dax%5E3+bx%5E2+cx+d++v%E1%BB%9Bi++a+l%C3%A0+s%E1%BB%91+nguy%C3%AAn+d%C6%B0%C6%A1ng+.+Bi%E1%BA%BFt+f+(5)+-+f+(+4+)+=2012+.++Ch%E1%BB%A9ng+minh+f+(7)+-+f+(2)+l%C3%A0+h%E1%BB%A3p+s%E1%BB%91+.&id=249516


Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)


a: Xét ΔABE và ΔADC có
AB=AD
\(\widehat{BAE}=\widehat{DAC}\)
AE=AC
Do đó: ΔABE=ΔADC



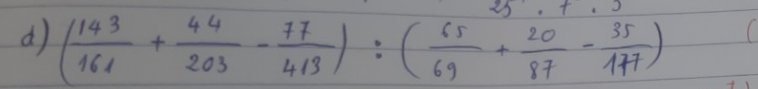


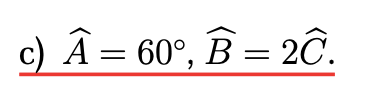

bạn vẽ hình được không.