
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(x-3)^3-(x+3)^3
= x^3 - 3^3 - x^3 + 3^3
= x^3 - x^3 - 9 + 9
= x^3 - x^3
= 0

a, \(A=x\left(2x^2-3-5x^2-x+x\right)=x\left(-3x-3\right)\)\(=-3x\left(x+1\right)\)
b, \(B=3x^2-6x-5x+5x^2-8x^2+24\)\(=-9x+24\)
C, \(C=x\left(2x^4-x^2-4x^4-2x^2+x-2x+6x^2\right)\)\(=x\left(-2x^4+3x^2-x\right)=-2x^5+3x^3-x^2\)
Chúc học tốt !
Lm ko chép lại đề


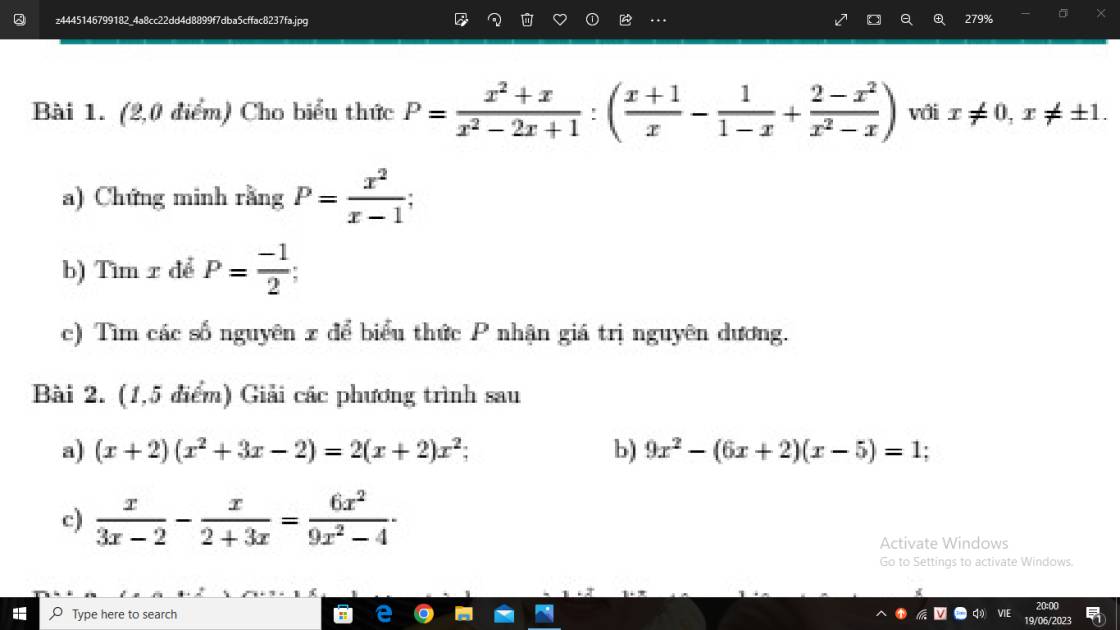
Bài 2 :
\(a,\left(x+2\right)\left(x^2+3x-2\right)=2\left(x+2\right)x^2\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2\right)-2x^2\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2-2x^2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\-x^2+3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x^2+x+2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x\left(x-1\right)+2\left(x-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left(x-1\right)\left(-x+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x-1=0\\-x+2=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\end{matrix}\right.\)
Vậy \(S=\left\{-2;2;1\right\}\)
\(b,9x^2-\left(6x+2\right)\left(x-5\right)=1\)
\(\Leftrightarrow9x^2-\left(6x^2-30x+2x-10\right)-1=0\)
\(\Leftrightarrow9x^2-6x^2+30x-2x+10-1=0\)
\(\Leftrightarrow3x^2+28x+9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-9\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{1}{3};-9\right\}\)
\(c,\dfrac{x}{3x-2}-\dfrac{x}{2+3x}=\dfrac{6x^2}{9x^2-4}\left(dkxd:x\ne\pm\dfrac{2}{3}\right)\)
\(\Leftrightarrow\dfrac{x}{3x-2}-\dfrac{x}{3x+2}-\dfrac{6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow\dfrac{x\left(3x+2\right)-x\left(3x-2\right)-6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow3x^2+2x-3x^2+2x-6x^2=0\)
\(\Leftrightarrow4x-6x^2=0\)
\(\Leftrightarrow-2x\left(-2+3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\-2+3x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=\dfrac{2}{3}\left(ktmdk\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
Bài 1 :
\(a,P=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\left(dkxd:x\ne0,x\ne\pm1\right)\)
\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2}{x-1}\left(dpcm\right)\)
\(b,P=-\dfrac{1}{2}\Rightarrow\dfrac{x^2}{x-1}=-\dfrac{1}{2}\)
\(\Rightarrow2x^2=-\left(x-1\right)\)
\(\Rightarrow2x^2=-x+1\)
\(\Rightarrow2x^2+x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
Vậy \(P=-\dfrac{1}{2}\) thì \(x=\dfrac{1}{2};x=-1\)
\(c,\) Để P nhận giá trị nguyên dương thì \(P\ge0\)
\(\Leftrightarrow\dfrac{x^2}{x-1}\ge0\Leftrightarrow x\ge0\)

Ta có: ab(a+b)-\(\frac{ab\left(a^3+b^3\right)}{a^2+2ab+b^2}\)
=\(ab\left(a+b\right)\)-\(\frac{ab\left(a^3+b^3\right)}{\left(a+b\right)^2}\)
=\(\frac{ab\left(a+b\right)^3}{\left(a+b\right)^2}\)-\(\frac{ab\left(a^3+b^3\right)}{\left(a+b\right)^2}\)
=\(\frac{ab\left[\left(a+b\right)^3-\left(a^3+b^3\right)\right]}{\left(a+b\right)^2}\)
=\(\frac{ab.3ab\left(a+b\right)}{\left(a+b\right)^2}\)
=\(\frac{3\left(ab\right)^2}{a+b}\)

3. gọi tử là x
mẫu là x + 8
Nếu thêm vào tử và bớt mẫu:
tử là x+2
mẫu là x+5
Ta có: \(\dfrac{x+2}{x+5}\)=\(\dfrac{3}{4}\)
4(x+2)=3(x+5)
4x + 8 = 3x + 15
x = 7
Tử số là 7
Mẫu số là x+8= 7+8= 15
Vậy phân số ban đầu l: \(\dfrac{7}{15}\)
2. \(\dfrac{3\left(x-2\right)}{6}\)- \(\dfrac{4}{6}\)> \(\dfrac{6x}{6}\)-\(\dfrac{6}{6}\)
<=> 3x - 6 - 4> 6x - 6
<=> 3x - 6 - 4 - 6x + 6> 0
<=> -3x -4 > 0
<=> -3x > 4
<=> x < \(\dfrac{-4}{3}\)
S= {x/x <\(\dfrac{-4}{3}\)}
trục số bạn tự vẽ giúp mình nhé

1
a
\(A=x^2-2x+4=x^2-2x+1+3\\=\left(x-1\right)^2+3\ge3\)
Min A = 3 khi và chỉ khi `x=1`
b
\(B=x^2+4x+5=x^2+4x+4+1\\ =\left(x+2\right)^2+1\ge1\)
Min B = 1 khi và chỉ khi `x=-2`
c
\(C=x^2+3x+4=x^2+3x+\dfrac{9}{4}+\dfrac{7}{4}\\ =\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
Min C = \(\dfrac{7}{4}\) khi và chỉ khi \(x=-\dfrac{3}{2}\)
d
\(D=3x^2-6x+4=3\left(x^2-2x+\dfrac{4}{3}\right)\\ =3\left(x^2-2x+1+\dfrac{1}{3}\right)\\ =3\left(x-1\right)^2+3.\dfrac{1}{3}\ge3.\dfrac{1}{3}\)
Min D = 1 khi và chỉ khi `x=1`

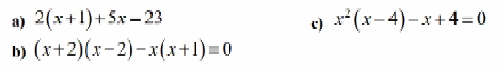


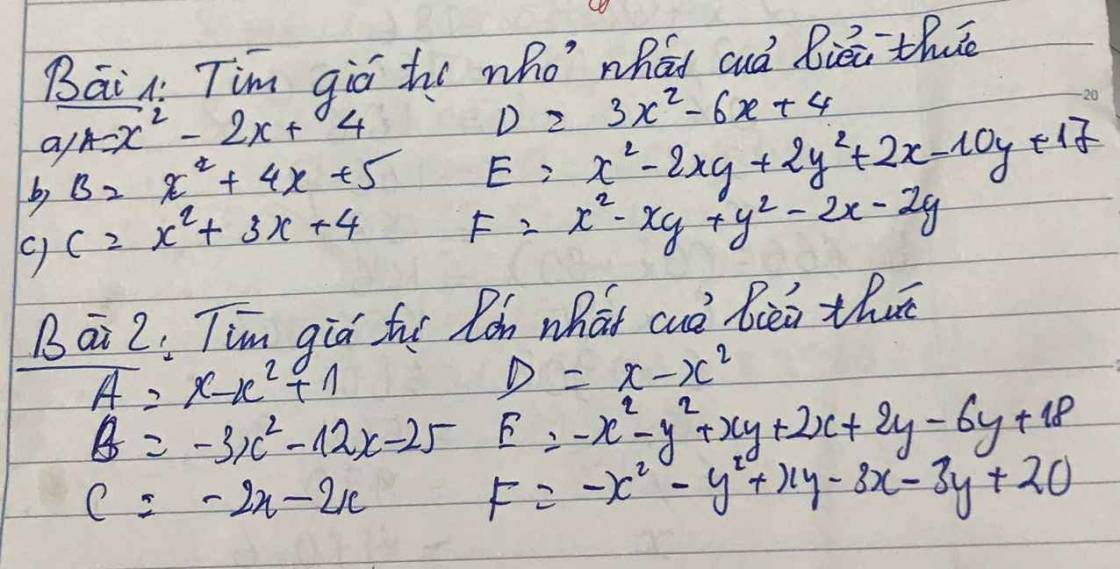
a) \(=3\left(xy-4\right)\)
b) \(=x^2\left(x-y\right)+4\left(x-y\right)=\left(x-y\right)\left(x^2+4\right)\)
c) \(=x^2-\left(y^2-12y+36\right)=x^2-\left(y-6\right)^2=\left(x-y+6\right)\left(x+y-6\right)\)
d) \(=\left(4p^2-36p+81\right)-25=\left(2p-9\right)^2-25=\left(2p-9-5\right)\left(2p-9+5\right)=4\left(p-7\right)\left(p-2\right)\)