Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho số tiền là x
thì giá của mặt hàng còn
100% - 20% = 80%
nên
sau khi hạ giá thì mua đc
x : 80% = x : 0,8 = 5x/4
nếu ko hạ giá thì mua đc
x : 100% = x
vậy hạ giá 20% thì = số tiền x thì có thể mua thêm
5x/4 - x = x/4
vậy hạ 20% thì mua thêm đc
x/4 : x = 1/4 = 25%
ok đó nha
cho số tiền là x
thì giá của mặt hàng còn
100% ‐ 20% = 80%
nên
sau khi hạ giá thì mua đc
x : 80% = x : 0,8 = 5x/4
nếu ko hạ giá thì mua đc
x : 100% = x
vậy hạ giá 20% thì = số tiền x thì có thể mua thêm
5x/4 ‐ x = x/4
vậy hạ 20% thì mua thêm đc
x/4 : x = 1/4 = 25%
ok đó nha

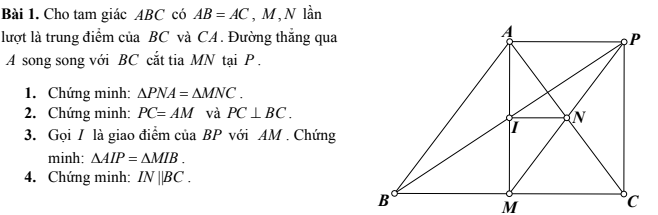
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC

1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)
--> tam giác AOC = tam giác BOD (c.g.c)
--> góc ACO = góc ODB
Mà 2 góc này ở vị trí so le trong
--> AC // BD

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC

1: Xét ΔAOC và ΔBOD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔAOC=ΔBOD
Suy ra: \(\widehat{ACO}=\widehat{BDO}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD