
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A

1.
\(\sqrt{2x+1}=x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+1\ge0\\2x+1=\left(x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\2x+1=x^2+4x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x^2+2x+3=0\left(vn\right)\end{matrix}\right.\)
Phương trình đã cho vô nghiệm
2.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
C1:
\(x^2-4x+21=6\sqrt{2x+3}\)
\(\Leftrightarrow\left(x^2-6x+9\right)+\left(2x+3-6\sqrt{2x+3}+9\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(\sqrt{2x+3}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\\sqrt{2x+3}-3=0\end{matrix}\right.\)
\(\Leftrightarrow x=3\)
C2:
\(x^2-4x+21=2.3.\sqrt{2x+3}\)
\(\Rightarrow x^2-4x+21\le3^2+2x+3\)
\(\Rightarrow x^2-6x+9\le0\)
\(\Rightarrow\left(x-3\right)^2\le0\)
\(\Rightarrow x-3=0\)
\(\Rightarrow x=3\)

3.
\(0\le sin^22x\le1\Rightarrow\dfrac{1+4.0}{5}\le y\le\dfrac{1+4.1}{5}\)
\(\Rightarrow\dfrac{1}{5}\le y\le1\)
\(y_{min}=\dfrac{1}{5}\) khi \(sin2x=0\Rightarrow x=\dfrac{k\pi}{2}\)
\(y_{max}=1\) khi \(cos2x=0\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
4.
\(y=2sin^2x-\left(1-2sin^2x\right)=4sin^2x-1\)
Do \(0\le sin^2x\le1\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=0\Rightarrow x=k\pi\)
\(y_{max}=3\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)


12:

a: Gọi M là trung điểm của BC
trên tia đối của tia MA, lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hình chữ nhật
=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
=>\(\overrightarrow{v}=\overrightarrow{AD}\)
b: \(\left|\overrightarrow{v}\right|=\left|\overrightarrow{AD}\right|=AD=2\cdot AM=2\cdot\dfrac{BC}{2}=BC=\sqrt{\left(6a\right)^2+\left(8a\right)^2}=10a\)
hình như đó đâu phải là câu 12 đâu ạ 🤔🤔🤔 trong đề câu 12 có chi tiết nào liên quan tới M đâu 🤔


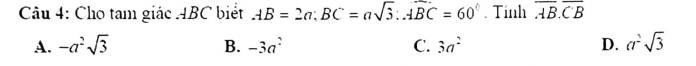
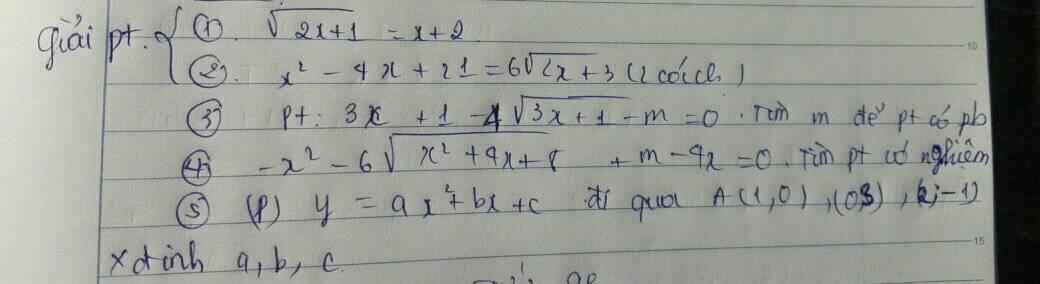 giúp em câu 3,4 với ạ
giúp em câu 3,4 với ạ giúp mình câu 3 với nha, giải ra luôn ạ
giúp mình câu 3 với nha, giải ra luôn ạ 
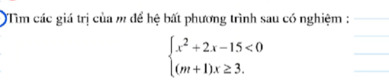
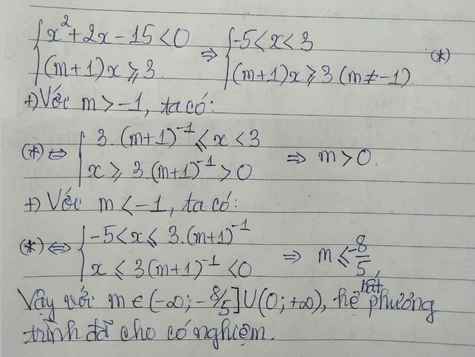


Bài 4 :
Áp dụng HTL trong tam giác vuông ABC :
\(AC^2=HC\cdot BC\)
\(\Leftrightarrow4^2=HC\cdot\left(HC+1.8\right)\)
\(\Leftrightarrow HC^2+1.8HC-16=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HC=3.2\left(N\right)\\HC=-5\left(L\right)\end{matrix}\right.\)
Bài 3 :
Áp dụng HTL trong tam giác vuông ABC :
\(AB^2=HB\cdot BC\)
\(\Leftrightarrow3^2=HB\cdot\left(HB+3.2\right)\)
\(\Leftrightarrow HB^2+3.2HB-9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HB=1.8\left(N\right)\\HB=-5\left(L\right)\end{matrix}\right.\)