K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 2
5: ĐKXĐ: \(\left\{{}\begin{matrix}x^2+3x-4>=0\\2x^2-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+4\right)\left(x-1\right)>=0\\2x\left(x-1\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=1\\x< =-4\end{matrix}\right.\\\left[{}\begin{matrix}x>=1\\x< =0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x>=1\\x< =-4\end{matrix}\right.\)
\(\sqrt{x^2+3x-4}< \sqrt{2x^2-2x}\)
=>\(x^2+3x-4< 2x^2-2x\)
=>\(2x^2-2x-x^2-3x+4>0\)
=>\(x^2-5x+4>0\)
=>(x-1)(x-4)>0
=>\(\left[{}\begin{matrix}x>4\\x< 1\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được:
\(\left[{}\begin{matrix}x>4\\x< =-4\end{matrix}\right.\)
7: ĐKXĐ: x>=-1
\(2\sqrt{x+2+2\sqrt{x+1}}-\sqrt{x+1}=4\)
=>\(2\cdot\sqrt{x+1+2\sqrt{x+1}+1}-\sqrt{x+1}=4\)
=>\(2\cdot\sqrt{\left(\sqrt{x+1}+1\right)^2}-\sqrt{x+1}=4\)
=>\(2\left(\sqrt{x+1}+1\right)-\sqrt{x+1}=4\)
=>\(\sqrt{x+1}+2=4\)
=>\(\sqrt{x+1}=2\)
=>x+1=4
=>x=3(nhận)
NN
1
HP
19 tháng 3 2021
ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)
19 tháng 1 2023
Câu 5:
ABCD là hình bình hành
=>vecto AB=vecto DC
=>\(\left\{{}\begin{matrix}4-x=2-0=2\\-1-y=1+3=4\end{matrix}\right.\Leftrightarrow D\left(2;-5\right)\)
Câu 6:
vecto c=k*vecto a+m*vecto b
=>\(\left\{{}\begin{matrix}-1=2k+3m\\7=-3k+m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=-2\\m=1\end{matrix}\right.\)
=>k+m=-1
Câu 7: B
Câu 8: C
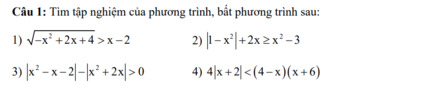
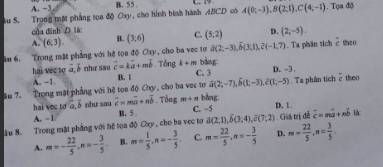
\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)
\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)
(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")
\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)
\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)
\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)
\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)
\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)
\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)
\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)