
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 15:
Gọi $x_0$ là nghiệm chung của 2 pt thì:
\(\left\{\begin{matrix}
x_0^2+ax_0+1=0\\
x_0^2-x_0-a=0\end{matrix}\right.\Rightarrow x_0(a+1)+(a+1)=0\)
\(\Leftrightarrow (x_0+1)(a+1)=0\)
Hiển nhiên $a\neq -1$ để 2 PT không trùng nhau. Do đó $x_0=-1$ là nghiệm chung của 2 PT
Thay vào:
$(-1)^2+a(-1)+1=0$
$\Leftrightarrow 1-a+1=0\Rightarrow a=2$
Đáp án C.
Câu 16:
D sai. Trong tam giác vuông tại $A$ là $ABC$, $\cos (90^0-\widehat{B})=\cos \widehat{C}$ và không có cơ sở để khẳng định $\cos \widehat{C}=\sin \widehat{C}$


\(9,=\dfrac{\sqrt{5}+1-\sqrt{5}+1}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{2}{4}=\dfrac{1}{2}\\ 10,=\dfrac{\sqrt{5}+2+\sqrt{5}-2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}=2\sqrt{5}\\ 11,=\dfrac{8+6\sqrt{2}-8+6\sqrt{2}}{\left(4-3\sqrt{2}\right)\left(4+3\sqrt{2}\right)}=\dfrac{12\sqrt{2}}{-2}=-6\sqrt{2}\\ 12,=\dfrac{2+\sqrt{6}+2-\sqrt{6}}{\left(2-\sqrt{6}\right)\left(2+\sqrt{6}\right)}=\dfrac{4}{-2}=-2\\ 13,=\sqrt{2}-1+\sqrt{2}+3=2\sqrt{2}+2\\ 14,=2-\sqrt{3}+\sqrt{3}-1=1\\ 15,=3-\sqrt{5}+\sqrt{5}-2=1\)


1) \(B=\dfrac{1}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{4-x}=\dfrac{1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{x-4}=\dfrac{1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}+2}{x-4}\)
Thay \(x=16\) vào biểu thức B ta được :
\(B=\dfrac{2\sqrt{x}+2}{x-4}=\dfrac{2\sqrt{16}+2}{16-4}=\dfrac{2\cdot4+2}{12}=\dfrac{10}{12}=\dfrac{5}{6}\)
2) \(P=\dfrac{B}{A}=\dfrac{\dfrac{2\sqrt{x}+2}{x-4}}{\dfrac{2}{\sqrt{x}+2}}=\dfrac{2\sqrt{x}+2}{x-4}\cdot\dfrac{\sqrt{x}+2}{2}=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\cdot2}=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
3)
\(P< 1\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 1\)
\(\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-1< 0\)
\(\Rightarrow\dfrac{\sqrt{x}+1-\left(\sqrt{x}-2\right)}{\sqrt{x}-2}< 0\)
\(\Rightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+2}{\sqrt{x}-2}< 0\)
\(\Rightarrow\dfrac{3}{\sqrt{x}-2}< 0\)
\(\Rightarrow\sqrt{x}-2< 0\)
\(\Rightarrow\sqrt{x}< 2\)
\(\Rightarrow x< 4\Rightarrow x\in\left\{0;1;2;3\right\}\)


1) Trong (O) có AE là dây cung không đi qua O có H là trung điểm AE
\(\Rightarrow OH\bot AE\Rightarrow\angle OHI=90\) mà \(\angle OBI=90\Rightarrow OBIH\) nội tiếp
2) OBIH nội tiếp \(\Rightarrow\angle BIO=\angle BHO\)
Vì \(AB\) là đường kính \(\Rightarrow\angle AEB=90\Rightarrow EB\bot AE\) mà \(OH\bot AE\)
\(\Rightarrow OH\parallel BE\Rightarrow \angle BHO=\angle HBE\Rightarrow \angle HBE=\angle BIO\)
3) Vì \(\left\{{}\begin{matrix}KH\bot AI\\AB\bot KI\end{matrix}\right.\Rightarrow\) O là trực tâm \(\Delta IAK\Rightarrow IO\bot AK\Rightarrow\angle ODA=90\)
mà \(\angle OHA=90\Rightarrow OHAD\) nội tiếp
Tương tự \(\Rightarrow\) ODKB,AHBK nội tiếp
Ta có: \(\angle HDO=\angle HAO=\angle HKB=\angle ODB\Rightarrow\) DI là phân giác \(\angle HDB\)

1) Gọi số xe mà công ty điều động đi chở hàng là a(xe) \(\left(a>0\right)\)
\(\Rightarrow\) mỗi xe dự định chở \(\dfrac{24}{a}\) (tấn hàng)
Theo đề: \(\dfrac{24}{a}=\dfrac{24}{a-2}-2\Rightarrow\dfrac{24}{a}=\dfrac{28-2a}{a-2}\Rightarrow24a-48=28a-2a^2\)
\(\Rightarrow2a^2-4a-48=0\Rightarrow a^2-2a-24=0\Rightarrow\left(a-6\right)\left(a+4\right)=0\)
mà \(a>0\Rightarrow a=6\)


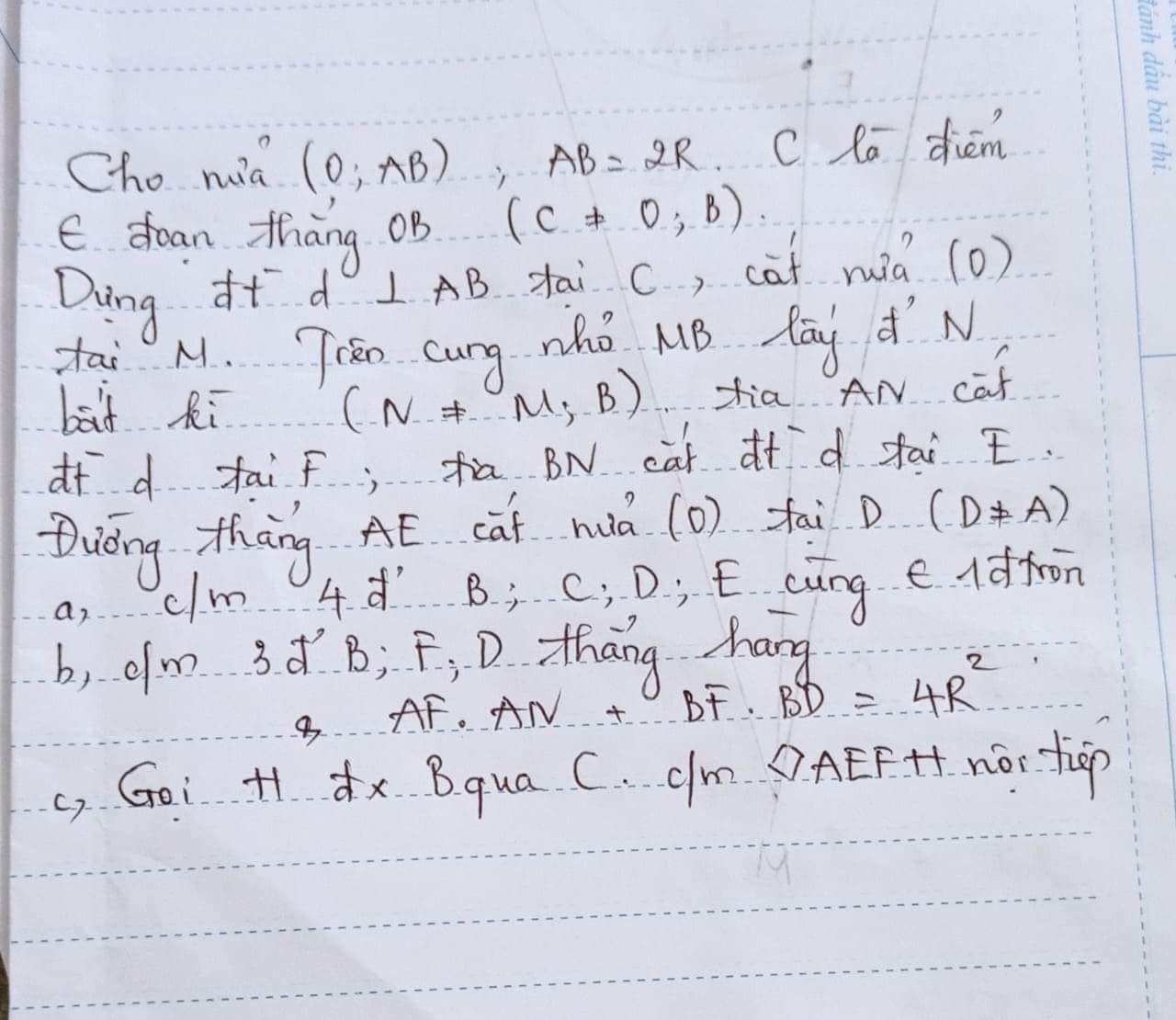
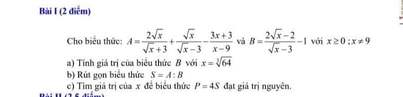

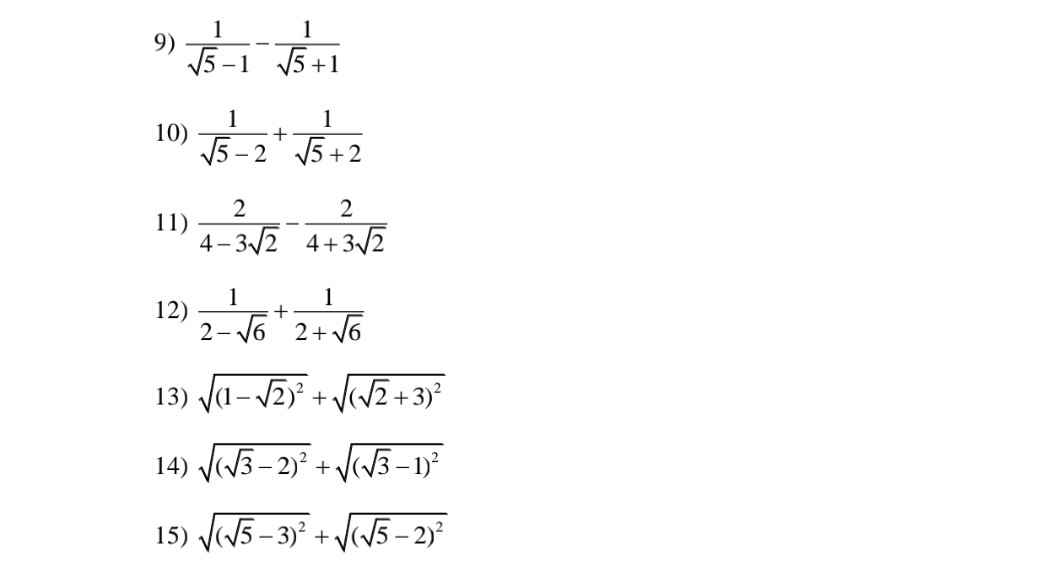




Lời giải:
Gọi số học sinh lớp 9/1 và 9/2 lần lượt là $a$ và $b$ (học sinh).
ĐK:...........
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=82\\ 4a+3b=286\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3a+3b=246\\ 4a+3b=286\end{matrix}\right.\)
\(\Rightarrow a=286-246=40\) (HS)
$b=82-a=42$ (HS)