
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


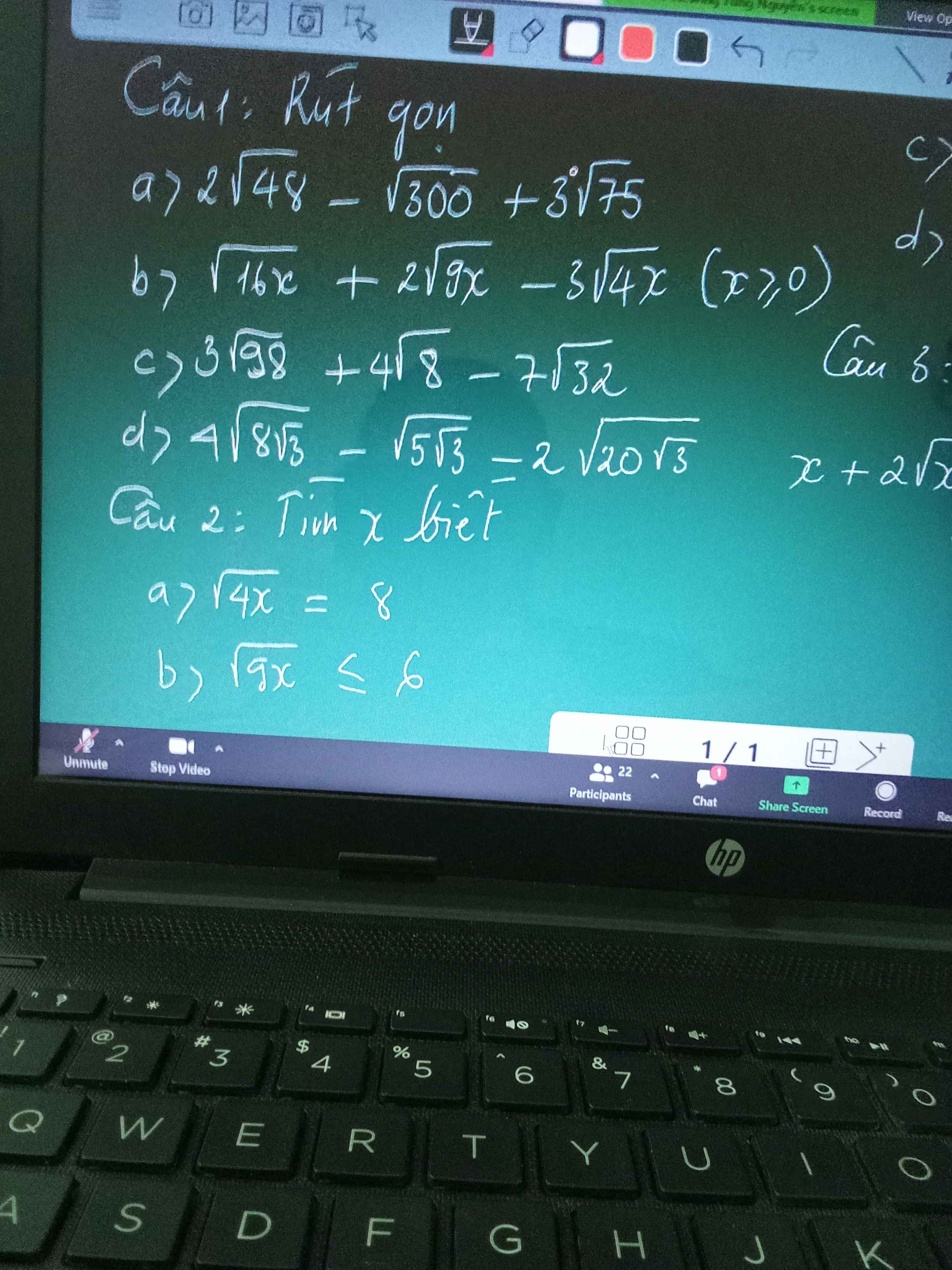
Câu 1
a)=\(8\sqrt{3}-10\sqrt{3}+15\sqrt{3}=13\sqrt{3}\)
b)=\(4\sqrt{x}+6\sqrt{x}-6\sqrt{x}=4\sqrt{x}\)
c)=\(21\sqrt{2}+8\sqrt{2}-28\sqrt{2}=\sqrt{2}\)
d)\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-\sqrt{5\sqrt{3}}-4\sqrt{5\sqrt{3}}\)
\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-5\sqrt{5\sqrt{3}}\)
câu 2
a)\(\Rightarrow4x=64\)\(\Rightarrow x=16\)
b)\(\Rightarrow9x\le36\)\(\Rightarrow x\le4\)
Câu 2:
a: Ta có: \(\sqrt{4x}=8\)
\(\Leftrightarrow4x=64\)
hay x=16
b: Ta có: \(\sqrt{9x}\le6\)
\(\Leftrightarrow9x\le36\)
\(\Leftrightarrow x\le4\)
Kết hợp ĐKXĐ, ta được: \(0\le x\le4\)

trong các số 11n+1010(n∈N*;n≤1010) có bao nhiêu số là số chính phương
mn giúp mk vs ạ
mk đang cần gấp


a: PK=căn 4*9=6cm
MN=4+9=13cm
MP=căn MK*MN=2*căn 13(cm)
NP=căn 9*13=3căn 13(cm)
b: MN=8^2:64/17=17(cm)
NP=căn 17^2-8^2=15(cm)
PK=8*15/17=120/17(cm)
NK=PN^2/NM=225/17(cm)

\(\Leftrightarrow\left\{{}\begin{matrix}x^3+2y^2-4y+3=0\\2x^2+2x^2y^2-4y=0\left(1\right)\end{matrix}\right.\Rightarrow}x^3+2y^2-4y-2x^2-2x^2y^2+4y=0\Rightarrow x^3+1-2x^2y^2+2y^2-2x^2+2=0\Rightarrow\left(x+1\right)\left(x^2-x+1\right)-2y^2\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(x^2-x+1-2xy^2+2y^2-2x+2\right)=0\Rightarrow x=-1\)Thay x=-1 vào (1) ta được y2-2y+1=0⇒ (y-1)2=0⇒y-1=0⇒y=1
Do đó Q=x2+y2=(-1)2+12=2

a) Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{3\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}+2}{\sqrt{a}+1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{3\sqrt{a}\left(\sqrt{a}+1\right)-\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{3a+3\sqrt{a}-\left(a-\sqrt{a}+2\sqrt{a}-2\right)}{\sqrt{a}}\)
\(=2+\dfrac{3a+3\sqrt{a}-a+\sqrt{a}-2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}+2a+2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\left(a+2\sqrt{a}+1\right)}{\sqrt{a}}\)
\(=\dfrac{2\left(\sqrt{a}+1\right)^2}{\sqrt{a}}\)
b) Ta có: \(P-6=\dfrac{2\left(\sqrt{a}+1\right)^2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2a+4\sqrt{a}+2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2\left(a-\sqrt{a}+1\right)}{\sqrt{a}}>0\forall a\) thỏa mãn ĐKXĐ
hay P>6

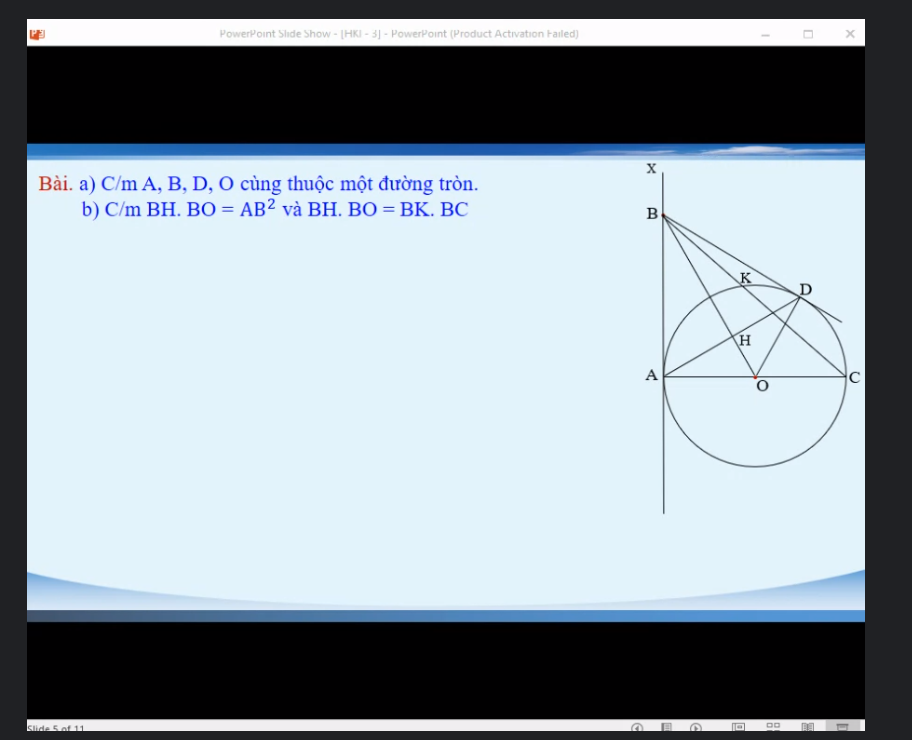
a: Xét tứ giác BAOD có
\(\widehat{BAO}+\widehat{BDO}=180^0\)
Do đó: BAOD là tứ giác nội tiếp




a)pt<=> \(-5\sqrt{x-2}=-2\)<=>\(5\sqrt{x-2}=2\)<=>\(25\left(x-2\right)=4\)(binh phuong 2 ve) <=> \(x-2=\frac{4}{25}\Rightarrow x=\frac{54}{25}\)vay \(x=\frac{54}{25}\)
b)pt<=> \(3\sqrt{x-1}=5-x\Leftrightarrow\sqrt{x-1}=\frac{5-x}{3}\Leftrightarrow x-1=\frac{25-10x+x^2}{9}\)\(\Leftrightarrow\frac{9x-9}{9}=\frac{25-10x+x^2}{9}\Leftrightarrow9x-9=25-10x+x^2\Leftrightarrow x^2-19x+34=0\)\(\Leftrightarrow x\left(x-2\right)-17\left(x-2\right)=0\Leftrightarrow\left(x-17\right)\left(x-2\right)=0\Rightarrow\orbr{\begin{cases}x-17=0\Rightarrow x=17\\x-2=0\Rightarrow x=2\end{cases}}\)vay \(x=17\)hoac \(x=2\)
c)pt \(\Leftrightarrow4x^2-12x+9=1\)(binh phuong 2 ve) \(\Leftrightarrow4x^2-12x+8=0\Leftrightarrow4x\left(x-2\right)-4\left(x-2\right)=0\Leftrightarrow4\left(x-1\right)\left(x-2\right)=0\Rightarrow\orbr{\begin{cases}x-1=0\Rightarrow x=1\\x-2=0\Rightarrow x=2\end{cases}}\)vay x=1 hoac x = 2