Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Nếu $x+y+z+t=0$ thì $M=\frac{-t}{t}=\frac{-x}{x}=\frac{-z}{z}=-1$
$\Rightarrow (M-1)^{2025}=(-1-1)^{2025}=(-2)^{2025}$
Nếu $x+y+z+t\neq 0$. Áp dụng TCDTSBN:
$M=\frac{x+y+z}{t}=\frac{y+z+t}{x}=\frac{z+t+x}{y}=\frac{t+x+y}{z}=\frac{x+y+z+y+z+t+z+t+x+t+x+y}{t+x+y+z}=\frac{3(x+y+z+t)}{x+y+z+t}=3$
$\Rightarrow (M-1)^{2025}=2^{2025}$

Bài 1:
a)\(\frac{2}{3}.\frac{5}{2}-\frac{3}{4}.\frac{2}{3}=\frac{5}{3}-\frac{1}{2}=\frac{7}{6}\)
b)\(2.\left(\frac{-3}{2}\right)^2-\frac{7}{2}=\frac{2.9}{4}-\frac{7}{2}=\frac{9-7}{2}=\frac{2}{2}=1\)
c)\(-\frac{3}{4}.\frac{68}{13}-0,75.\frac{36}{13}=\frac{-3.4.17}{4.13}-\frac{3.9.4}{4.13}=\frac{-51-27}{13}=\frac{-78}{13}=-6\)
Bài 2:
a)|x-1,4|=1,6
\(\Rightarrow\left[\begin{array}{nghiempt}x-1,4=1,6\\x-1,4=-1,6\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=3\\x=-0,2\end{array}\right.\)
b) \(\frac{3}{4}-x=\frac{4}{5}\)
\(x=\frac{3}{4}-\frac{4}{5}=-\frac{1}{20}\)
c)(1-2x)3=-8
(1-2x)3=(-2)3
1-2x=-2
2x=3
x=\(\frac{3}{2}\)
Bài 3:
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{7}=k\)
\(\Rightarrow\begin{cases}x=2k\\y=5k\\z=7k\end{cases}\)
A=\(\frac{2k-5k+7k}{2k+2.5k-7k}=\frac{4k}{5k}=\frac{4}{5}\)
=> x=4/5 . 2= 8/5
y=4/5 . 5=4
z=4/5.7=28/5

\(B=\dfrac{10\cdot9}{\sqrt{10}}-2\cdot5+1+2021=9\sqrt{10}-10+2022=9\sqrt{10}+2012\)

\(A=-\dfrac{1}{6}-\left[\dfrac{9}{16}-\dfrac{9}{8}+\dfrac{3}{4}\right]\)
\(=\dfrac{-1}{6}-\dfrac{9-18+12}{16}=\dfrac{-1}{6}-\dfrac{3}{16}\)
\(=\dfrac{-8}{48}-\dfrac{9}{48}=-\dfrac{17}{48}\)

\(B=\left(-\dfrac{3}{4}+\dfrac{3}{4}\right)^2+\dfrac{3}{4}\cdot\dfrac{-5}{9}+7^3\)
=-15/36+343
=343-5/12=4111/12

\(=64\cdot\dfrac{-1}{8}+100\cdot\dfrac{1}{100}\)
=-8+1
=-7

\(\frac{3}{5}.\left(\frac{5}{3}-\frac{2}{7}\right)-\left(\frac{7}{3}-\frac{3}{7}\right).\frac{3}{5}\)
\(=\frac{3}{5}.\text{[}\left(\frac{5}{3}-\frac{2}{7}\right)-\left(\frac{7}{3}-\frac{3}{7}\right)\text{]}\)
\(=\frac{3}{5}.\text{[}\frac{5}{3}-\frac{2}{7}-\frac{7}{3}+\frac{3}{7}\text{]}\)
\(=\frac{3}{5}.\text{[}\left(\frac{5}{3}-\frac{7}{3}\right)-\left(\frac{2}{7}-\frac{3}{7}\right)\text{]}\)
\(=\frac{3}{5}.\text{[}\frac{-2}{3}-\frac{-1}{7}\text{]}\)
\(=\frac{3}{5}.\left(\frac{-2}{3}+\frac{1}{7}\right)\)
\(=\frac{3}{5}.\left(\frac{-14}{21}+\frac{3}{21}\right)\)
\(=\frac{3}{5}.\frac{-11}{21}\)
\(=\frac{3.\left(-11\right)}{5.21}\)
\(=\frac{-11}{5.7}=\frac{-11}{35}\)
Chúc bạn học tốt

Gọi số hs thik thể thao, âm nhạc, thời trang ll là \(a,b,c(a,b,c\in \mathbb{N^*})\)
Áp dụng tc dtsbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{c-b}{5-3}=\dfrac{6}{2}=3\\ \Rightarrow\left\{{}\begin{matrix}a=6\\b=9\\c=15\end{matrix}\right.\)
Vậy ...
Gọi số hs thích thể thao; âm nhạc; thời trang lần lượt là \(x;y;z\)
Theo đề : \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\) và \(z-y=6hs\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có :
\(\dfrac{z}{5}-\dfrac{y}{3}=\dfrac{z-y}{5-3}=\dfrac{6}{3}=2\)
Ta có : \(\dfrac{x}{2}=3\Rightarrow x=3.2=6\left(hs\right)\)
\(\dfrac{y}{3}=3\Rightarrow y=3.3=9\left(hs\right)\)
\(\dfrac{z}{5}=3\Rightarrow z=3.5=15\left(hs\right)\)
Vậy : Số hs thích thể thao : \(6hs\)
Âm nhạc : \(9hs\)
Thời trang: \(15hs\)




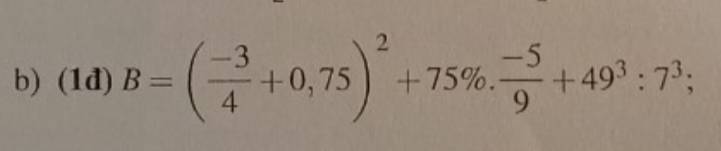

\(=\left(\dfrac{1}{2}+\dfrac{1}{2}\right)-\left(\dfrac{5}{41}+\dfrac{36}{41}\right)=1-1=0\)