
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Xét △OBC có: \(BC\)//\(AD\) (gt).
=>\(\dfrac{OD}{OC}=\dfrac{OA}{OB}\) (định lí Ta-let).
=>\(OD=\dfrac{OA}{OB}.OC=\dfrac{2,5}{2}.3=3,75\) (cm).

Tớ ko giúp đc)): cọu tự tra google đuy,chứ có google để làm j ((:?

Gọi số ly trà sữa là x
=>Số ly trà đào là 210-x
Theo đề, ta có: 27000x=2*18000(210-x)
=>27000x-36000(210-x)=0
=>27000x-7560000+36000x=0
=>x=120
=>Số ly trà đào là 90 ly


Lời giải:
$4x-6=2x+4$
$\Leftrightarrow (4x-6)-(2x+4)=0$
$\Leftrightarrow 2x-10=0$
$\Leftrightarrow 2x=10$
$\Leftrightarrow x=5$

c) Ta có: \(P=2x+\dfrac{1}{x+1}\)
\(\Leftrightarrow\dfrac{-x}{x+1}=2x+\dfrac{1}{x+1}\)
\(\Leftrightarrow\dfrac{-x}{x+1}=\dfrac{2x\left(x+1\right)+1}{x+1}\)
Suy ra: \(2x^2+2x+1=-x\)
\(\Leftrightarrow2x^2+3x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\left(loại\right)\\x=-\dfrac{1}{2}\left(nhận\right)\end{matrix}\right.\)
Vậy: Để \(P=2x+\dfrac{1}{x+1}\) thì \(x=-\dfrac{1}{2}\)
`a)F=((x+1)/(1-x)-(1-x)/(x+1)-(4x^2)/(x^2-1)):(4x^2-4)/(x^2-2x+1)`
`đk:x ne +-1`
`F=((-(x+1)^2+(x-1)^2-4x^2)/(x^2-1)):(4(x-1)(x+1))/(x-1)^2`
`=(-x^2-2x-1+x^2-2x+1-4x^2)/(x^2-1):(4(x+1))/(x-1)`
`=(-4x^2-4x)/((x-1)(x+1)).(x-1)/(4(x+1))`
`=(-4(x-1))/((x-1)(x+1)).(x-1)/(4(x+1))`
`=-4/(x+1).(x-1)/(4(x+1)`
`=(1-x)/(x+1)^2`
`F<-1`
`<=>(1-x-(x+1)^2)/(x+1)^2<0`
Vì `(x+1)^2>0`
`=>1-x-(x+1)^2<0`
`<=>(x+1)^2+x-1>0`
`<=>x^2+2x+1+x-1>0`
`<=>x^2+3x>0`
`<=>x(x+3)>0`
`<=>` $\left[ \begin{array}{l}x>0\\x<-3\end{array} \right.$
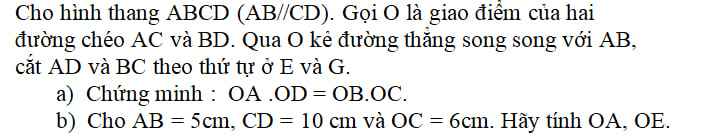



 giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ
giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ



a) Vì AB // CD ⇒ \(\widehat{ABD}=\widehat{ODC}\) ( 2 góc so le trong )
Hay \(\widehat{ABO}=\widehat{ODC}\)
Xét △ AOB và △ COD có:
\(\widehat{ABO}=\widehat{CDO}\) ( chứng minh trên )
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh )
⇒ △ AOB ∼ △ COD ( g - g )
b) Vì △ AOB ∼ △ COD
⇒ \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\Rightarrow\dfrac{OA}{6}=\dfrac{5}{10}\)
\(\Rightarrow OA=3cm\)
Vì OE // DC nên theo định lí Ta - lét ta có:
\(\dfrac{OE}{BC}=\dfrac{OA}{AC}\Rightarrow\dfrac{OE}{10}=\dfrac{3}{3+6}\)
\(\Rightarrow OE\approx3,3cm\)