
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi số cây lớp 7A,7B,7C lần lượt là a,b,c(cây;a,b,c∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{180}{12}=15\\ \Leftrightarrow\left\{{}\begin{matrix}a=45\\b=60\\c=75\end{matrix}\right.\)
Vậy ...
hỏi nhá,theo đại lượng tỉ lệ thuận vẫn làm như thế này hả bạn ?


1 m dây thép nặng:
2,4 :1,5 = 1,6 kg
60 m dây thép nặng :
1,6 . 60=96(kg)

Hình 1:
Ta có: AD\(\perp\)AB
CB\(\perp\)AB
Do đó: AD//CB
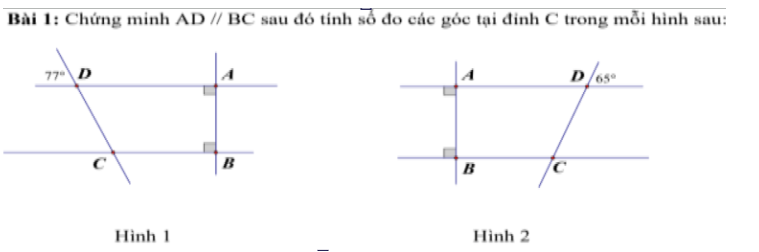
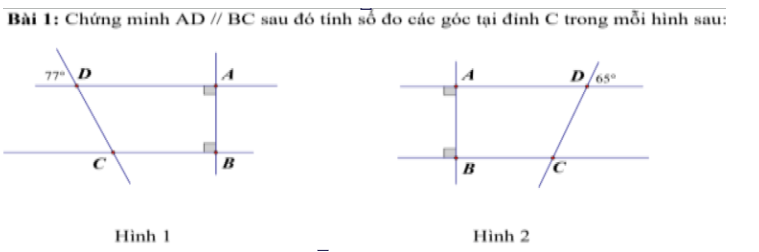
Hình 2:
Ta có: \(AD\perp AB\)
BC\(\perp\)AB
Do đó: AD//BC
Ta có :
\(A\perp D;A\perp B;B\perp C\)
\(\Rightarrow\)AD//CB
\(\widehat{C1}=\widehat{D1}\) (đồng vị)
\(\Rightarrow\widehat{C1}=77^o\)
\(\Rightarrow\widehat{C2}=180^o-77^o=103^o\) (trong cùng phía)
\(\widehat{C4}=\widehat{C2}\) (đối đỉnh)
\(\Rightarrow\widehat{C4}=103^o\)
\(\widehat{C3}=\widehat{C3}\) (đối đỉnh)
\(\Rightarrow\widehat{C3}=77^o\)

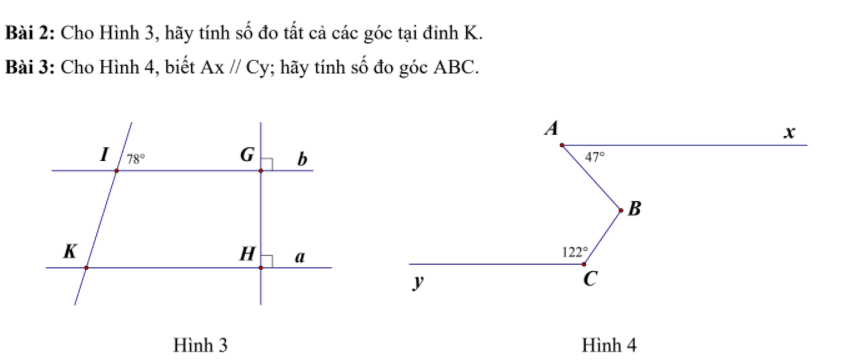
Bài 2:
Vì $b\perp GH, a\perp GH\Rightarrow a\parallel b$
Do đó:
$\widehat{K_1}=\widehat{I_1}=78^0$ (hai góc đồng vị)
$\widehat{K_2}=\widehat{K_1}=78^0$ (hai góc đối đỉnh)
$\widehat{K_4}=180^0-\widehat{K_1}=180^0-78^0=102^0$ (hai góc kề bù)
$\widehat{K_3}=\widehat{K_4}=102^0$ (đối đỉnh)
Bài 3: Kẻ tia $Bt\parallel Ax$. Vì $Ax\parallel Cy$ nên $Bt\parallel Cy$
Ta có:
$\widehat{B_1}=\widehat{BAx}=47^0$ (hai góc so le trong)
$\widehat{B_2}+\widehat{BCy}=180^0$ (trong cùng phía)
$\Rightarrow \widehat{B_2}=180^0-\widehat{BCy}=180^0-122^0=58^0$
Do đó: $\widehat{ABC}=\widehat{B_1}+\widehat{B_2}=47^0+58^0=105^0$

a, \(\dfrac{x}{4}=\dfrac{y}{7};xy=112\)
Ta có: \(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x.y}{4.7}=\dfrac{112}{28}=4\)
*\(\dfrac{x}{4}=4=>x=16\)
*\(\dfrac{y}{7}=4=>y=28\)
Vậy (x, y)\(\in\){ 16, 28}
Nhiều quá, nên tách ra nha
e, \(\dfrac{x}{-9}=\dfrac{y}{4};xy=-36\)
Ta có: \(\dfrac{x}{-9}=\dfrac{y}{4}=\dfrac{xy}{\left(-9\right).4}=\dfrac{-36}{-36}=1\)
* \(\dfrac{x}{-9}=1=>x=-9\)
* \(\dfrac{y}{4}=1=>y=4\)
Vậy( x, y) ∈{ -9; 4}



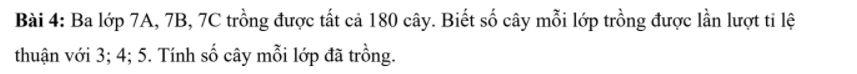
 giúp tớ tớ cần gấp
giúp tớ tớ cần gấp
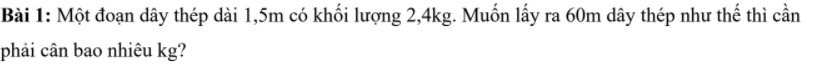
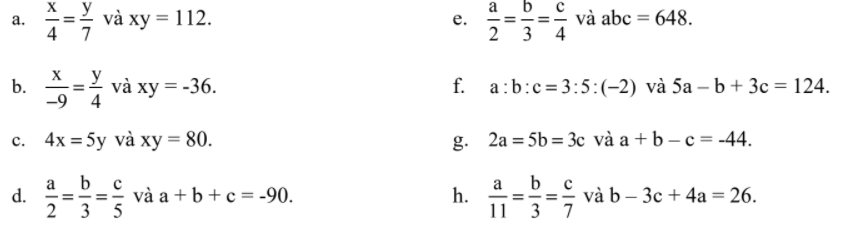

Ta có :
\(xy=\frac{1}{6};yz=\frac{1}{12};zx=\frac{1}{8}\)
\(\Rightarrow xy.yz.zx=\frac{1}{6}.\frac{1}{12}.\frac{1}{8}\)
\(\Rightarrow x^2.y^2.z^2=\frac{1}{576}\)
\(\Rightarrow\left(x.y.z\right)^2=\left(\frac{1}{24}\right)^2=\left(\frac{1}{-24}\right)^2\)
\(\Rightarrow\orbr{\begin{cases}x.y.z=\frac{1}{24}\\x.y.z=\frac{1}{-24}\end{cases}}\)
Với x.y.z = \(\frac{1}{24}\)mà xy = \(\frac{1}{6}\)
\(\Rightarrow z=\frac{1}{4}\)mà \(yz=\frac{1}{2}\)\(\Rightarrow y=2\)
Mà xy = \(\frac{1}{6}\)=> x = \(\frac{1}{12}\)
Với x.y.z = \(\frac{1}{-24}=\frac{-1}{24}\)mà xy = \(\frac{1}{6}\)
\(\Rightarrow z=\frac{-1}{4}\)mà \(yz=\frac{1}{2}\)=> y = -2
Mà xy = \(\frac{1}{6}\)=> x = \(\frac{-1}{12}\)
olm ơi tương tác xíu đi mờ