
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x2 + x + 1
= x 2 +2x +1 - x
= (x + 1 )2 - \(\sqrt{x}\)2
= ( x + 1 - \(\sqrt{x}\) ) (x + 1 + \(\sqrt{x}\))
\(x^2+x+1=\left[x^2+2.\frac{1}{2}x+\left(\frac{1}{2}\right)^2\right]+\left(\frac{\sqrt{3}}{2}\right)^2\)
\(=\left(x^2+\frac{1}{2}\right)-\left(\frac{\sqrt{3}}{2}\right)^2\)
\(=\left(x^2+\frac{1}{2}-\frac{\sqrt{3}}{2}\right)\left(x^2+\frac{1}{2}+\frac{\sqrt{3}}{2}\right)\)
\(=\left(x^2+\frac{1-\sqrt{3}}{2}\right)\left(x^2+\frac{1+\sqrt{3}}{2}\right)\)
Tham khảo nhé~

Bài 1
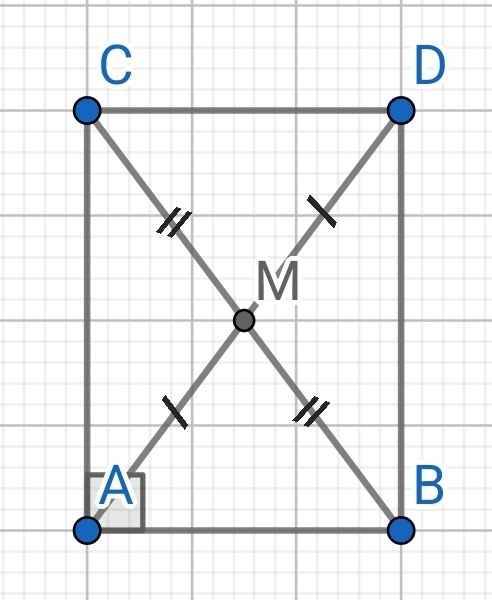 a) Do AM là đường trung tuyến của ∆ABC
a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông
Bài 2
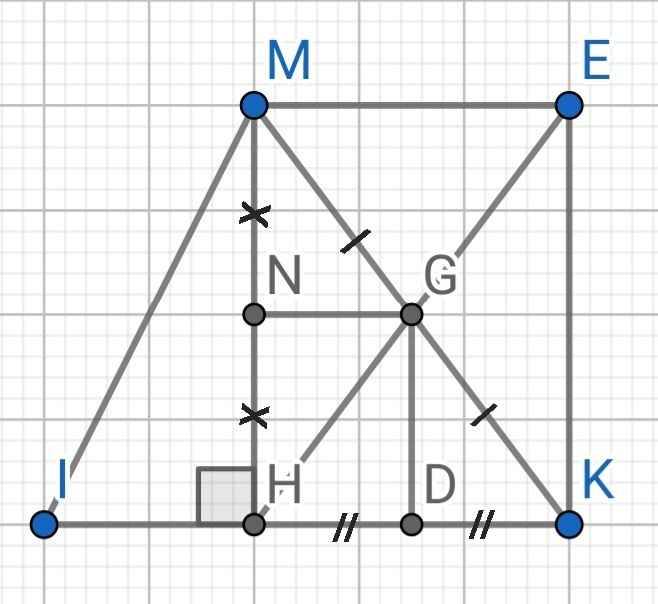 a) Do H và E đối xứng với nhau qua G (gt)
a) Do H và E đối xứng với nhau qua G (gt)
⇒ G là trung điểm của HE
Tứ giác MEKH có:
G là trung điểm HE (cmt)
G là trung điểm MK (gt)
⇒ MEKH là hình bình hành
Mà ∠MHK = 90⁰ (MH ⊥ IK)
⇒ MEKH là hình chữ nhật
b) ∆MHK có:
N là trung điểm MH (gt)
G là trung điểm MK (gt)
⇒ NG là đường trung bình của ∆MHK
⇒ NG // HK và NG = HK : 2
Do D là trung điểm HK
⇒ HD = HK : 2
⇒ HD = NG = HK : 2
Do NG // HK
⇒ NG // HD
Do ∠MHK = 90⁰
⇒ ∠NHD = 90⁰
Tứ giác NGDH có:
NG // HD (cmt)
NG = HD (cmt)
⇒ NGDH là hình bình hành
Mà ∠NHD = 90⁰ (cmt)
⇒ NGDH là hình chữ nhật

Khogn6 trả lời giúp mình thì đừng có nhắn lung tung H24 H là j z

suy ra (x-2)(2x+1)=2-x=-(x-2)
<=>(x-2)(2x+1)+(x-2)=0
<=>(x-2)(2x+1)=0
<=>x-2=0 hoặc 2x+1=0
<=> x=2 hoặc x=-1/2
Vậy tập nghiệm của phương trình là .........

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

n^3 + 20n = n^3 - 4n + 24n
n^3 + 20n = n.(n² - 4) + 24n
n^3 + 20n = n.(n - 2).(n+2) + 24n
n = 2k
=> n^3 + 20n = 8k.(k - 1).(k+1) + 48k
ta có: k.(k-1).(k+1) là tích 3 stn liên tiếp => chia hết cho 2.3 = 6
=> 8k.(k - 1).(k+1) chia hết 8.6 = 48 => n^3 +20n chia hết cho 48.

Ta có: ΔABC∼ΔDEF
nên DE/AB=EF/BC=DF/AC
=>9/6=EF/10=DF/14
=>EF/10=DF/14=3/2
=>EF=15cm; DF=21cm

Bài 1:
Để B là số tự nhiên thì \(\left\{{}\begin{matrix}2x-10⋮x-1\\\left[{}\begin{matrix}x>5\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\\x< 0\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{-1;-3;-7\right\}\)





 Giúp mình làm bài này với ạ
Giúp mình làm bài này với ạ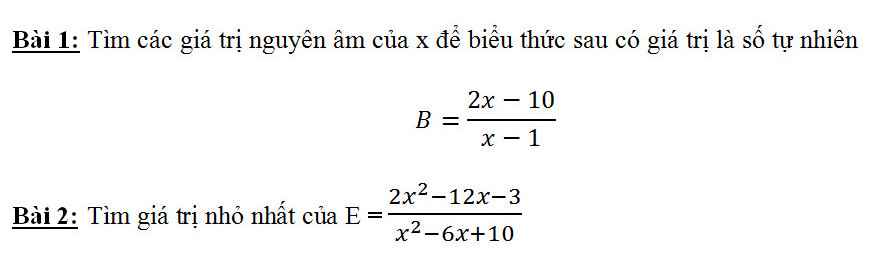
\(a.4x^2-20x-4x^2+3x-4x+3=5\)
\(-17x+3=5\)
\(-17x=2\)
\(x=-\frac{2}{17}\)
\(4x\left(x-5\right)-\left(x-1\right)\left(4x-3\right)=5\)
\(\Leftrightarrow4x^2-20x-4x^2-\left(4x^2-3x-4x+3\right)=5\)
\(\Rightarrow4x^2-20x-4x^2+7x+3=5\)
\(\Leftrightarrow-13x+3-5=0\)
\(\Leftrightarrow x=-\frac{2}{13}\)