
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(g,ĐK:x\ge0\\ PT\Leftrightarrow10\sqrt{x}+8\sqrt{x}-11\sqrt{x}=21\\ \Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ h,ĐK:x\ge0\\ PT\Leftrightarrow6\sqrt{3x}+2\sqrt{3x}-3\sqrt{3x}=15\\ \Leftrightarrow\sqrt{3x}=5\Leftrightarrow3x=25\Leftrightarrow x=\dfrac{25}{3}\left(tm\right)\)

2:
a: \(A=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-6}{3}=-2\)
b: \(B=\dfrac{\left(x_1+x_2\right)^2-3x_1x_2}{1-x_1x_2}=\dfrac{36-3\cdot3}{1-3}=\dfrac{36-9}{-2}=-\dfrac{27}{2}\)
c: \(C=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-6\right)^2-4\cdot3}=2\sqrt{6}\)
d: \(D=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-3x_1x_2\)
\(=\left(-6\right)^3-3\cdot3\cdot\left(-6\right)-3\cdot3\)
=261

a: Xét (O) có
DA,DB là tiếp tuyến
nên OD là phân giác của góc AOB(1) và DA=DB
Xét (O) có
EA,EC là tiếp tuyến
nên OE là phân giác của góc COA(2) và EC=EA
Từ (1), (2) suy ra góc EOD=1/2*180=90 độ
b: DE=AD+AE
=>DE=BD+CE

m = b3+b3
= (a+b ) (a2+b2+ ab)
mà a+b bằng 1 nên
m=a2+b2 - ab
m= (a^2 + b^2 + 2ab ) - 3ab
3ab = _ < 3 (a+b ) 2/4
=> m _>- 3 (a+b ) 2/4
=1- 3/4 = 3/4
chả cần j cả lm bff của nhau thui :3

câu 3 Gọi vận tốc ban đầu là x(x>0)km/h
vân tốc tăng thêm khi đi 100km là x+10 km/h
thời gian đi hết 100km là \(\dfrac{100}{x}h\)
thời gian đi hết quãng đường còn lại là \(\dfrac{220-100}{x+10}h\)
vì tổng tg đi hết quãng đường AB là 4h nên ta có pt
\(\dfrac{100}{x} \)+\(\dfrac{220-100}{x+10}\)=4
giải pt x=50
vậy vận tốc ban đầu đi là 50 km/h
Gọi x (km/h) là vận tốc ban đầu của ô tô (x > 0)
\(\Rightarrow\) x + 10 (km/h) là vận tốc lúc sau của ô tô
Thời gian đi 100 km đầu là: \(\dfrac{100}{x}\) (h)
Thời gian đi hết quãng đường còn lại là: \(\dfrac{220-100}{x+10}=\dfrac{120}{x+10}\) (h)
Theo đề bài ta có phương trình:
\(\dfrac{100}{x}+\dfrac{120}{x+10}=4\)
\(\Leftrightarrow100\left(x+10\right)+120x=4x\left(x+10\right)\)
\(\Leftrightarrow100x+1000+120x=4x^2+40x\)
\(\Leftrightarrow4x^2+40x-220x-1000=0\)
\(\Leftrightarrow4x^2-180x-1000=0\)
\(\Leftrightarrow x^2-45x-250=0\)
\(\Delta=\left(-45\right)^2-4.1.\left(-250\right)=3025\)
\(\Rightarrow\Delta=55\)
\(x_1=\dfrac{-\left(-45\right)+55}{2.1}=50\) (nhận)
\(x_2=\dfrac{-\left(-45\right)-55}{2.1}=-5\) (loại)
Vậy vận tốc ban đầu của ô tô là 50 km/h

Bài 3:
a: Xét ΔMNE vuông tại M và ΔDPE vuông tại P có
\(\widehat{MEN}=\widehat{DEP}\)
Do đó: ΔMNE\(\sim\)ΔDPE
b: Xét ΔEDP vuông tại D và ΔPDN vuông tại D có
\(\widehat{EPD}=\widehat{PND}\left(=\widehat{MNE}\right)\)
Do đó: ΔEDP\(\sim\)ΔPDN
Bài 2:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=64\)
hay AC=8cm
Xét ΔABC có
H là trung điểm của AB
I là trung điểm của BC
Do đó: HI là đường trung bình của ΔBAC
Suy ra: HI//AC và \(HI=\dfrac{AC}{2}\)
hay \(HI=\dfrac{8}{2}=4\left(cm\right)\)
b: Xét tứ giác AHMC có
AC//MH
AC=MH
Do đó: AHMC là hình bình hành
mà \(\widehat{CAH}=90^0\)
nên AHMC là hình chữ nhật


5) \(=\dfrac{5\left(\sqrt{21}+4\right)}{21-16}+\dfrac{-\sqrt{21}\left(\sqrt{7}-\sqrt{3}\right)}{\sqrt{7}-\sqrt{3}}\)
\(=\sqrt{21}+4-\sqrt{21}=4\)
6) \(=\dfrac{8\left(3-\sqrt{5}\right)}{9-5}-\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}\)
\(=6-2\sqrt{5}-\sqrt{5}=6-3\sqrt{5}\)
\(5.\dfrac{5}{\sqrt{21}-4}+\dfrac{3\sqrt{7}-7\sqrt{3}}{\sqrt{7}-\sqrt{3}}\\ =\dfrac{5\left(\sqrt{21}+4\right)}{21-16}+\dfrac{\sqrt{3}.\sqrt{7}\left(\sqrt{7}-\sqrt{3}\right)}{\sqrt{7}-\sqrt{3}}\\ =\dfrac{5\left(\sqrt{21}+4\right)}{5}+\sqrt{21}\\ =\sqrt{21}+4+\sqrt{21}=4+2\sqrt{21}\)
\(6.\dfrac{8}{3+\sqrt{5}}-\dfrac{\sqrt{15}-2\sqrt{5}}{\sqrt{3}-2}\\ =\dfrac{8\left(3-\sqrt{5}\right)}{9-5}-\dfrac{\left(\sqrt{15}-2\sqrt{5}\right)\left(\sqrt{3}+2\right)}{3-4}\\ =2\left(3-\sqrt{5}\right)+\sqrt{15}.\sqrt{3}+2\sqrt{15}-2\sqrt{15}-4\sqrt{5}\\ =6-2\sqrt{5}+3\sqrt{5}+2\sqrt{15}-2\sqrt{15}-4\sqrt{5}\\ =6-3\sqrt{5}\)

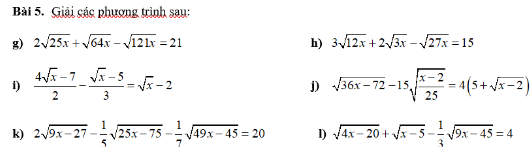





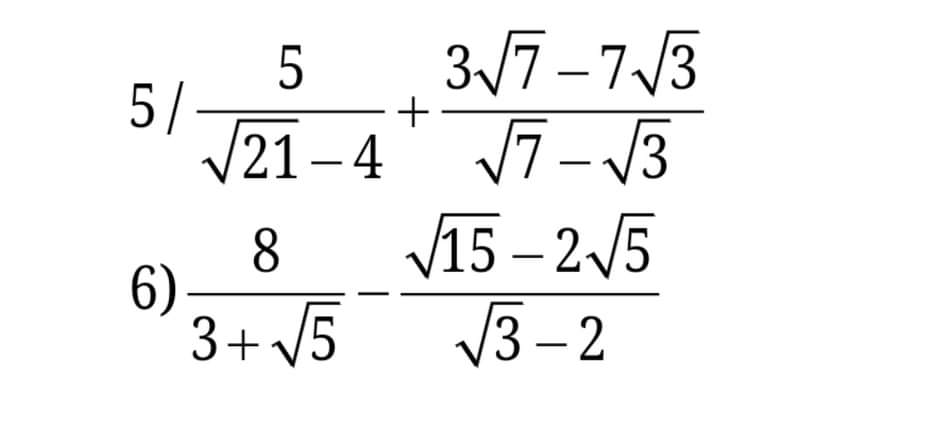 giúp mình với, cảm ơn
giúp mình với, cảm ơn