
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: \(15x^2y-10xy^2=5xy\left(3x-2y\right)\)
b: \(x^2+2xy+y^2-9=\left(x+y-3\right)\left(x+y+3\right)\)

1: Ta có: \(3\left(x+5\right)-2\left(4-3x\right)=7\)
\(\Leftrightarrow3x+15-8+6x=7\)
\(\Leftrightarrow9x=14\)
hay \(x=\dfrac{14}{9}\)
2: Ta có: \(x\left(7-2x\right)+2x\left(x-2\right)=15\)
\(\Leftrightarrow7x-2x^2+2x^2-4x=15\)
\(\Leftrightarrow3x=15\)
hay x=5
3: Ta có: \(2x\left(9x-4\right)-9x\left(2x-3\right)=-38\)
\(\Leftrightarrow18x^2-8x-18x^2+27x=-38\)
\(\Leftrightarrow19x=-38\)
hay x=-2
7: Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x-5\right)^2=30\)
\(\Leftrightarrow x^2-5-x^2+10x-25=30\)
\(\Leftrightarrow10x=60\)
hay x=6
8: Ta có: \(\left(x+2\right)\left(x-2\right)+8=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-4+8=x^2-2x+1\)
\(\Leftrightarrow-2x=3\)
hay \(x=-\dfrac{3}{2}\)

=>2(2x+1)-2x+3>=6
=>4x+2-2x+3>=6
=>2x+5>=6
=>2x>=1
=>x>=1/2

d) . đkxđ : x khác 0 , x khác -5
\(\Leftrightarrow\left(2x+5\right)\left(x+5\right)=2x.x\)
<=> \(2x^2+10x+5x+25=2x^2\)
<=> \(2x^2+15x+25-2x^2=0\)
<=> \(15x+25=0\)
<=> \(15x=-25\Rightarrow x=\dfrac{-25}{15}=-\dfrac{5}{3}\left(nhận\right)\)
Vậy.....
e).
\(\left|x+2\right|=3x+5\Leftrightarrow\left\{{}\begin{matrix}x+2=3x+5\left(khi\right)x+2\ge0\Leftrightarrow x\ge-2\left(1\right)\\-\left(x+2\right)=3x+5\left(khi\right)x+2< 0\Leftrightarrow x< -2\left(2\right)\end{matrix}\right.\)
Giải pt ( 1) khi \(x\ge-2\) :
\(x+2=3x+5\\ \Leftrightarrow x+2-3x-5=0\\ \Leftrightarrow-2x-3=0\)
<=> \(-2x=3\)
\(\Rightarrow x=\dfrac{-3}{2}\left(nhận\right)\)
Giải pt (2) khi \(x< -2\) :
\(-\left(x+2\right)=3x+5\)
\(\Leftrightarrow-x-2-3x-5=0\)
<=> \(-4x-7=0\)
<=> \(-4x=7\)
<=> \(x=\dfrac{-7}{4}\left(loại\right)\)
Vậy \(S=\left\{-\dfrac{3}{2}\right\}\)
f).
\(\left(2x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Vậy ..
\(\dfrac{2x+5}{2x}=\dfrac{x}{x+5}\)
\(\Leftrightarrow\dfrac{\left(2x+5\right)\left(x+5\right)-2x^2}{2x\left(x+5\right)}=0\)
\(\Leftrightarrow2x^2+10x+5x+25-2x^2=0\)
\(\Leftrightarrow15x=-25\)
\(\Leftrightarrow x=-\dfrac{5}{3}\)
\(\left|x+2\right|=3x+5\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=3x+5\\x+2=-3x-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2-3x-5=0\\x+2+3x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x-3=0\\4x+7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=-\dfrac{7}{4}\end{matrix}\right.\)
\(\left(2x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)

a: MNPQ là hình bình hành
=>MQ//NP
=>MQ//IP
Xét tứ giác MIPQ có IP//MQ
nên MIPQ là hình thang
b: ΔMNP vuông cân tại N
=>MN=NP và \(\widehat{MNP}=90^0\)
Hình bình hành MNPQ có \(\widehat{MNP}=90^0\)
nên MNPQ là hình chữ nhật
=>\(\widehat{Q}=\widehat{P}=90^0\)
Xét ΔMNI vuông tại N có \(sinNMI=\dfrac{NI}{MN}=\dfrac{2}{3}\)
nên \(\widehat{NMI}\simeq42^0\)
\(\widehat{NMI}+\widehat{QMI}=\widehat{NMQ}=90^0\)
=>\(\widehat{QMI}+42^0=90^0\)
=>\(\widehat{QMI}=48^0\)
IP//MQ
=>\(\widehat{QMI}+\widehat{MIP}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{MIP}+48^0=180^0\)
=>\(\widehat{MIP}=132^0\)

\(x^2-y^2-z^2-2yz\)
\(=x^2-\left(y^2+2yz+z^2\right)\)
\(=x^2-\left(y+z\right)^2\)
\(=\left(x-y-z\right)\left(x+y+z\right)\)
P/S: nếu đề là phân tích thành nhân tử thì lm như thế nhé

gọi thời gian đi cùa xe máy là x ( h , 0<x<4,5)
khi đó thời gian về của xe là 4,5-x
theo bài ra ta có phương trình:
30 x = 24 ( 4,5-x )
\(\Leftrightarrow\)x = 2
vậy quãng đường AB dài 2 x 30 =60 (km)

Câu 70: B
Câu 1: C
Câu 2: A
Cau 3: A
Câu 6: B
Câu 7: B
Câu 8: C
Câu 9: C
Câu 10: B


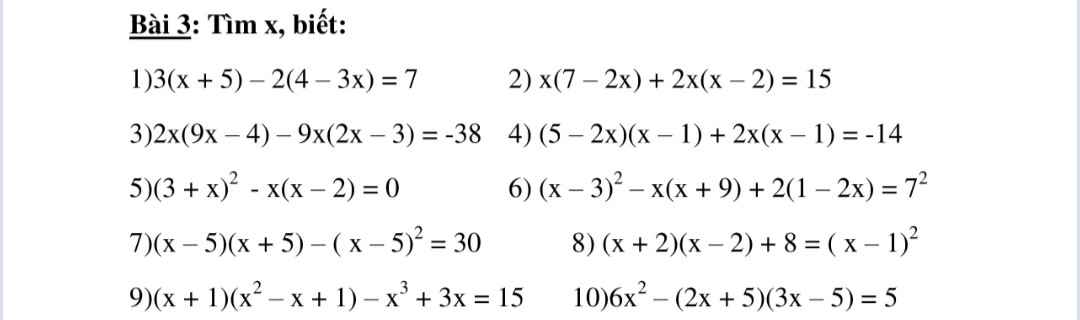

 giai pt giup minh voi a
giai pt giup minh voi a

\(a,\) Vì ABCD là hbh nên \(\widehat{A}=\widehat{C}=120^0\)
Mà AB//CD và ABCD là hbh nên \(\widehat{B}=\widehat{D}=180^0-\widehat{A}=60^0\)
\(b,\) Vì ABCD là hbh nên AD//BD do đó \(\widehat{C}+\widehat{D}=180^0\left(trong.cùng.phía\right)\)
Mà \(\widehat{C}-\widehat{D}=30^0\Rightarrow\left\{{}\begin{matrix}\widehat{C}=\left(180^0+30^0\right):2=105^0\\\widehat{D}=180^0-105^0=75^0\end{matrix}\right.\)
Mà ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{A}=\widehat{C}=105^0\\\widehat{B}=\widehat{D}=75^0\end{matrix}\right.\)
\(c,\) Vì ABCD là hbh nên AD//BC do đó \(\widehat{A}+\widehat{B}=180^0\)
Ta có \(\widehat{A}:\widehat{B}=4:5\Rightarrow\dfrac{\widehat{A}}{4}=\dfrac{\widehat{B}}{5}\)
Áp dụng t/c dtsbn:
\(\dfrac{\widehat{A}}{4}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{A}+\widehat{B}}{9}=\dfrac{180^0}{9}=20^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=80^0\\\widehat{B}=100^0\end{matrix}\right.\)
Mà ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{A}=\widehat{C}=80^0\\\widehat{B}=\widehat{D}=100^0\end{matrix}\right.\)