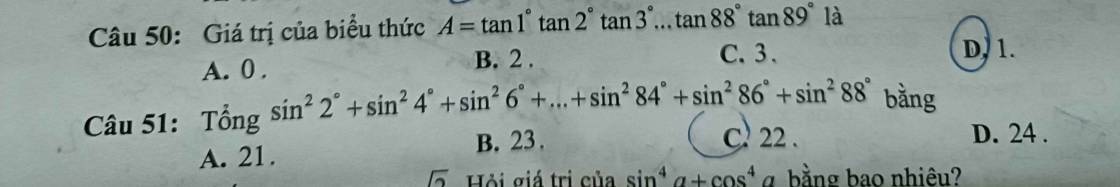Sử dụng bất đẳng thức AM-GM ta có:

\(\hept{\begin{cases}a^n+\left(n-1\right)\left(\frac{a+b+c}{3}\right)^n\ge n\sqrt[n]{a^n\left(\frac{a+b+c}{3}\right)^{n\left(n-1\right)}}=n\left(\frac{a+b+c}{3}\right)^{n-1}a\\b^n+\left(n-1\right)\left(\frac{a+b+c}{3}\right)^n\ge n\sqrt[n]{b^n\left(\frac{a+b+c}{3}\right)^{n\left(n-1\right)}}=n\left(\frac{a+b+c}{3}\right)^{n-1}b\\c^n+\left(n-1\right)\left(\frac{a+b+c}{3}\right)^n\ge n\sqrt[n]{c^n\left(\frac{a+b+c}{3}\right)^{n\left(n-1\right)}}=n\left(\frac{a+b+c}{3}\right)^{n-1}c\end{cases}}\)

_________________________________________________________________________________________

\(\Rightarrow\left(a^n+b^n+c^n\right)\ge n\left(\frac{a+b+c}{3}\right)^{n-1}\left(a+b+c\right)-3\left(n-1\right)\left(\frac{a+b+c}{3}\right)^n\)\(=3\left(\frac{a+b+c}{3}\right)^n\)

Câu 50 thì bạn nhóm cặp lại tan1*tan89*tan2*tan88*...*tan45

thì bạn sẽ thấy là tan1*tan89=tan2*tan88=...=tan45=1

=>D

Câu 51 thì bạn nhóm cặp lại \(sin^288^0;sin^22^0\); sin²86⁰ và sin²4⁰;...;sin²44 độ và sin² 46 độ thì bạn sẽ thấy từng cặp đó có tổng bằng 1

Và có 22 cặp như vậy nên đáp án là C

Lấy phần cần lấy thôi nha, t hết giấy nháp rồi :)))

Câu 5: 

\(\Leftrightarrow-x^2+7x-9+2x-9=0\)

\(\Leftrightarrow x^2-9x+18=0\)

=>x=3

=>Chọn A