
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


$ĐKXĐ : x \neq 2, x \neq -2$
Ta có : $1+\dfrac{2}{x-2} = \dfrac{2x^2}{x^2-4}$
$\to \dfrac{x^2-4+2.(x+2)}{(x-2).(x+2)} = \dfrac{2x^2}{(x-2).(x+2)}$
$\to x^2-4+2.(x+2) = 2x^2$
$\to x^2 -2x - 8 = 0 $
$\to (x-4).(x+2) = 0 $
$\to x = 4$ ( Do $x \neq -2, 2$ )
Vậy \(S=\left\{4\right\}\)

\(a.A=\left(\dfrac{x}{x^2-4}+\dfrac{1}{x+2}-\dfrac{2}{x-2}\right):\left(1-\dfrac{x}{x+2}\right)\left(đk:x\ne\pm2\right)\)
\(=\left[\dfrac{x}{x^2-4}+\dfrac{x-2}{x^2-4}-\dfrac{2\left(x+2\right)}{x^2-4}\right]:\left(\dfrac{x+2}{x+2}-\dfrac{x}{x+2}\right)\)
\(=\dfrac{x+x-2-2x-4}{x^2-4}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{\left(x+2\right)\left(x-2\right)}.\dfrac{x+2}{2}\)
\(=\dfrac{-3}{x-2}\left(1\right)\)
\(b.\) Thay x = 2023 vào (1), ta được:
\(\dfrac{-3}{2023-2}=-\dfrac{3}{2021}\)
\(c.\) Để A là một số nguyên thì \(x-2\inƯ_{\left(-3\right)}\)
Vậy x - 2 có các giá trị sau:
\(\left[{}\begin{matrix}x-2=1\\x-2=-1\\x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\\x=5\\x=-1\end{matrix}\right.\)

.- Đề Toán nhé,chứ máy đt mình bận sạc rồi,nên ko chụp đc hình
Câu 1 : Thực hiện các phép tính :
a) \(-2x^3.\left(x^2+5x-\dfrac{1}{2}\right)\)
b) \(\left(20x^4y-25x^2y^2-3x^2y\right):5x^2y\)
c) \(\dfrac{x+3}{3xy^2}:\dfrac{4x+12}{x^2y}\)
Câu 2 : Phân tích đa thức thành nhân tử :
a) \(x^3-4x\)
b) \(x^2+6x+9-25y^2\)
c) \(x^2-11x+30\)
Câu 3 :
Cho biểu thức : \(A=\left(\dfrac{1}{x-1}+\dfrac{x}{x^2-1}\right):\dfrac{2x+1}{x^2+2x+1}\)
a) Tìm điều kiện của x để A được xác định.
b) Rút gọn A.
c) Tìm giá trị nguyên của x để A có giá trị nguyên
Câu 4 : Cho 2 đa thức : \(A=x^3-1\) và \(B= x- 1\)
Tìm giá trị nhỏ nhất của \(\dfrac{A}{B}\)
Câu 5 : Cho tam giác ABC vuông tại A,đường trung tuyến AD.Gọi E là điểm đối xứng với A qua D,M là trung điểm của cạnh AC.
a) Tứ giác ABEC là hình gì ? Vì sao ?
b) Cho AB = 5cm.Tính MD
c) Gọi N là chân đường vuông góc kẻ từ C đến đường thẳng BM
Chứng minh : \(AN\perp EN\)

a) (2x - 7)/4x + (3 + 4x)/4x
= (2x - 7 + 3 + 4x)/4x
= (6x - 4)/4x
= (3x - 2)/2x
b) (9x - 5)/(x² + x) + (10 - 4x)/(x² + x)
= (9x - 5 + 10 - 4x)/[x(x + 1)]
= (5x + 5)/[x(x + 1)]
= 5(x + 1)/[x(x + 1)]
= 5/x
c) (3x - 9)/(x - 1) : (x² - 9)/(x² - 2x + 1)
= 3(x - 3)/(x - 1) . (x - 1)²/[(x - 3)(x + 3)
= 3(x - 1)/(x + 3)

 giúp vs ạ mốt là thi rồi
giúp vs ạ mốt là thi rồi  giúp mình bài 3 vs mn ơi ko phải thi chỉ là đề ôn thôi ạ
giúp mình bài 3 vs mn ơi ko phải thi chỉ là đề ôn thôi ạ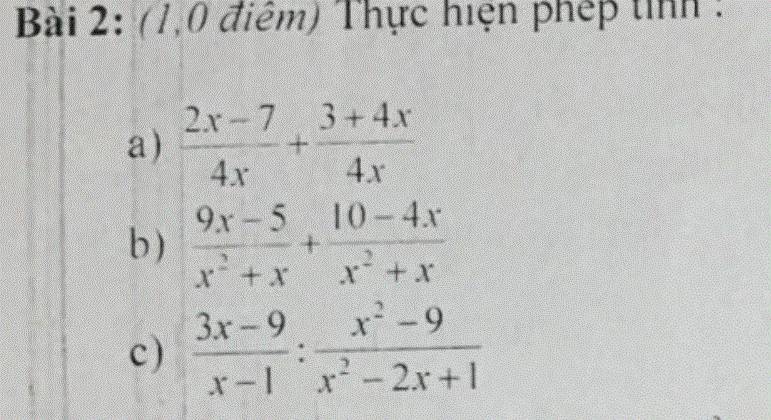



a: Xet ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
DO đó: ΔAHD=ΔCKB
=>AH=KC
mà AH//KC
nên AHCK là hình bình hành
b: Vì ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC
AHCK là hình bình hành
nên AC cắt HK tại trung điểm của mỗi đường
=>H đối xứng K qua O