
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét (B;BA) có
BA là bán kính
CA vuông góc BA tại A
Do đó: CA là tiếp tuyến của (B;BA)

Xét ΔABC có
BE,CF là đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếpΔABC
=>d(I;BC)=d(I;AB)=d(I;AC) và AI là phân giác của góc BAC
ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC tại D
=>d(I;BC)=ID
=>d(I;AB)=d(I;AC)=ID
=>AB,AC là tiếp tuyến của (I;ID)

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{BOM}\)
\(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
b: CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
c: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\) không đổi

a: T=20*5000-500=99500(ngàn đồng)
b: T=9000*8=72000
Số sản phẩm bán được sẽ thỏa mãn:
20n-500=72000
=>n-25=3600
=>n=3625


1: \(=\left(\dfrac{\sqrt{x}+2}{2\left(\sqrt{x}-2\right)}-\dfrac{4\sqrt{x}}{x-4}\right):\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{x+4\sqrt{x}+4-8\sqrt{x}}{2\left(x-4\right)}\cdot\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)^2\cdot\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\)
3: \(=\dfrac{x+\sqrt{x}-5\sqrt{x}+3}{x-1}\cdot\dfrac{2\sqrt{x}+6-4}{\sqrt{x}+3}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}+3}=\dfrac{2\left(\sqrt{x}-3\right)}{\sqrt{x}+3}\)


 giúp e với ạaa
giúp e với ạaa
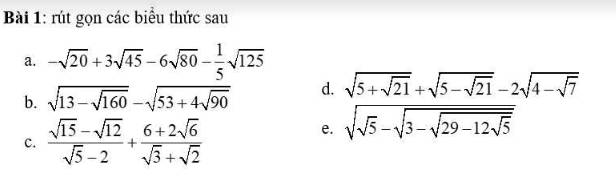 giúp e với ạaa
giúp e với ạaa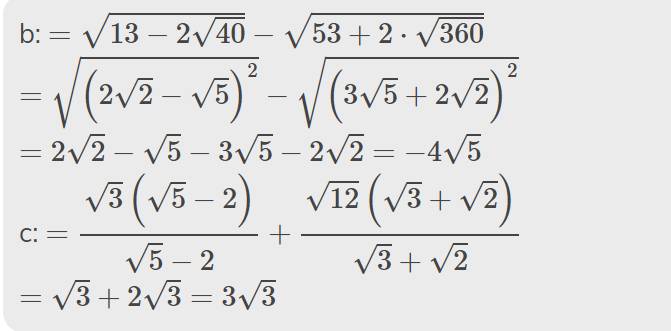
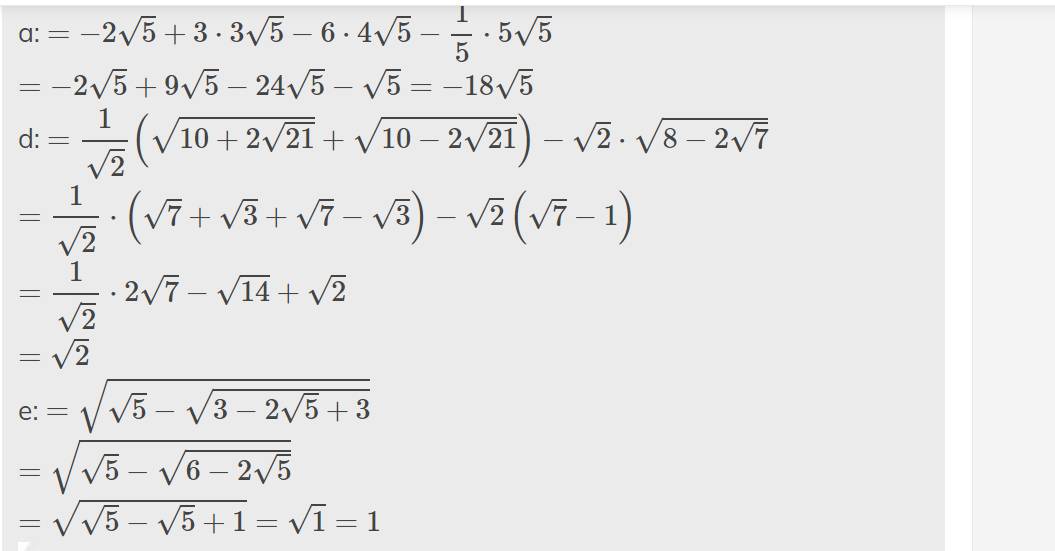
 giúp e gấp với ạaa
giúp e gấp với ạaa giúp e gấp với ạaa
giúp e gấp với ạaa

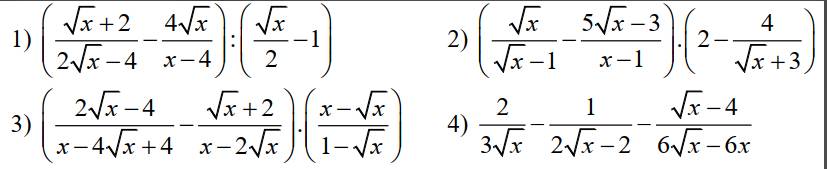 giúp e bài này với ạaa
giúp e bài này với ạaa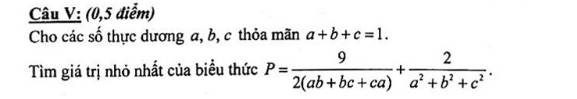 giúp e vs ạaa
giúp e vs ạaa
a. Em tự giải
b.
Ta có: \(\widehat{ABC}=\widehat{AQC}\) (cùng chắn AC) (1)
Do AQ là đường kính \(\Rightarrow\widehat{ACQ}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACQ}=90^0\) \(\Rightarrow\widehat{ACQ}+\widehat{CAQ}=90^0\) (2)
Tam giác ABD vuông tại D \(\Rightarrow\widehat{BAD}+\widehat{ABC}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{CAQ}=\widehat{BAD}\)
c.
\(\left\{{}\begin{matrix}\widehat{PAE}=\widehat{PAI}+\widehat{CAQ}\\\widehat{IAB}=\widehat{PAI}+\widehat{BAD}\\\widehat{CAQ}=\widehat{BAD}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{PAE}=\widehat{IAB}\) (3)
Tứ giác BCEF nội tiếp (E và F cùng nhìn BC dưới 1 góc vuông)
\(\Rightarrow\widehat{ABI}+\widehat{CEF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEP}=180^0\)
\(\Rightarrow\widehat{AEP}=\widehat{ABI}\) (4)
(3);(4) \(\Rightarrow\Delta AEP\sim\Delta ABI\left(g.g\right)\)
\(\Rightarrow\dfrac{AP}{AI}=\dfrac{AE}{AB}\) (5)
AQ là đường kính \(\Rightarrow\widehat{ABQ}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ABQ}=90^0\)
Xét 2 tam giác ABQ và AEH có: \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{AEH}=90^0\\\widehat{BAQ}=\widehat{EAH}\left(\text{theo (3)}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABQ\sim\Delta AEH\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AQ}\) (6)
(5);(6) \(\Rightarrow\dfrac{AH}{AQ}=\dfrac{AP}{AI}\) \(\Rightarrow\dfrac{AP}{AH}=\dfrac{AI}{AQ}\)
\(\Rightarrow PI||HQ\) (định lý Talet đảo)