Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
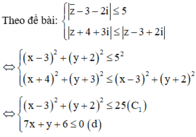
=> Tập hợp các điểm biểu diễn số phức z là miền mặt phẳng (T) mà tọa độ các điểm thỏa mãn hệ (*)
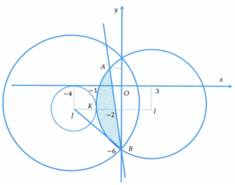
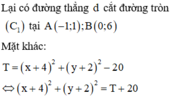


Giả sử z = x + yi có điểm M (x;y) biểu diễn z trên mặt phẳng (Oxy).
Ta có z - 1 + i = x - 1 + y + 1 i ; z + 1 - 2 i = x + 1 + - y - 2 i
Theo đề bài
z - 1 + i = z + 1 - 2 i ⇔ x - 1 2 + y + 1 2 = x - 1 2 + - y - 2 2 ⇔ x - 1 2 + y + 1 2 = x - 1 2 + y + 2 2 ⇔ x 2 - 2 x + 1 + y 2 + 1 = x 2 + 2 x + 1 + y 2 + 4 y + 4
Do đó tập hợp các điểm biểu diễn của z là đường thẳng ∆ : 4 x + 2 y + 3 = 0
Suy ra a = 4; b = 2; c = 3 Vậy ab + c = 11
Đáp án C

Chọn A.
Gọi I(0;2) và M z ⇒ M I = 5 suy ra tập điểm biểu diễn của số phức z trong mặt phẳng tọa độ giao điểm của đường tròn (C) tâm I(0;2) bán kính R = 5 và
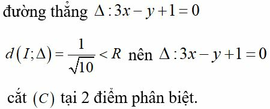

Đáp án B.
Phương pháp: Tính độ dài đoạn thẳng IM với I là tâm mặt cầu.
Tham số hóa tọa độ điểm M, sau đó dựa vào độ dài IM để tìm điểm M.
Cách giải : Mặt cầu (S) có tâm I(1;2; – 3) bán kính R = 3 3
Đặt MA = MB = MC = a
Tam giác MAB đều => AB = a
Tam giác MBC vuông tại M => BC = a 2
Tam giác MCA có C M A ^ = 120 0 => AC = a 3
Xét tam giác ABC có A B 2 + B C 2 = A C 2 => ∆ABC vuông tại B
=>∆ABC ngoại tiếp đường tròn nhỏ có đường kính AC
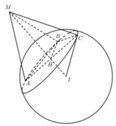
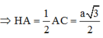
Xét tam giác vuông IAM có:
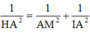
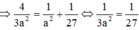
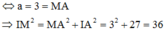
![]()
![]()
![]()
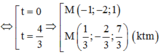
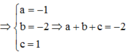
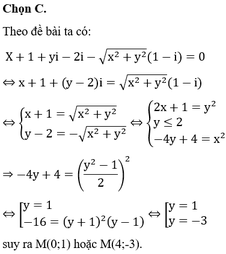
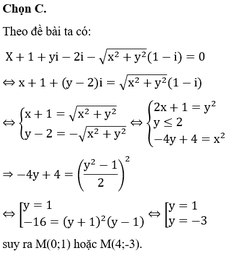


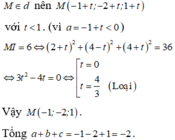

Chọn đáp án B.