Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử có phương án sắp xếp các số từ 1 đến 10 vào các đỉnh và các cạnh của ngũ giác sao cho tổng các số trên mỗi cạnh đều bằng nhau và bằng S.
Khi đó, ta lấy tổng tất cả 5 cạnh bằng 5.S và trong tổng này các số trên các cạnh được tính một lần, còn các số trên các đỉnh được tính hai lần. Ta gọi tổng các số trên 5 đỉnh là T, ta có:
5.S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + T
Hay là:
S = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + T)/5 = 11 + T/5
Vậy để S nhỏ nhất có thể thì T cũng phải nhỏ nhất, mà tổng T có 5 số trong các số {1,2, ..., 10} nên T nhỏ nhất khi T = 1 + 2 + 3 + 4 + 5 = 15.
Khi đó S = 11 + T/15 = 11 + 15/5 = 14
Hay nói cách khác, tổng các số trên mỗi cạnh nhỏ nhất bằng 14 khi đặt các số 1, 2, 3, 4, 5 trên các đỉnh của ngũ giác. Dưới đây là một phương án thỏa mãn điều kiện này.
19482105736
Giả sử có phương án sắp xếp các số từ 1 đến 10 vào các đỉnh và các cạnh của ngũ giác sao cho tổng các số trên mỗi cạnh đều bằng nhau và bằng S.
Khi đó, ta lấy tổng tất cả 5 cạnh bằng 5.S và trong tổng này các số trên các cạnh được tính một lần, còn các số trên các đỉnh được tính hai lần. Ta gọi tổng các số trên 5 đỉnh là T, ta có:
5.S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + T
Hay là:
S = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + T)/5 = 11 + T/5
Vậy để S nhỏ nhất có thể thì T cũng phải nhỏ nhất, mà tổng T có 5 số trong các số {1,2, ..., 10} nên T nhỏ nhất khi T = 1 + 2 + 3 + 4 + 5 = 15.
Khi đó S = 11 + T/15 = 11 + 15/5 = 14
Hay nói cách khác, tổng các số trên mỗi cạnh nhỏ nhất bằng 14 khi đặt các số 1, 2, 3, 4, 5 trên các đỉnh của ngũ giác. Dưới đây là một phương án thỏa mãn điều kiện này.

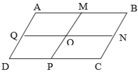
a) Hình trên có tất cả 9 hình bình hành
b) Chu vi hình bình hành ABCD bằng: (4 + 6) x 2 = 20cm
Chu vi hình bình hành AMOQ, BMON, DPOQ và NOPC là: 20 : 4 = 5cm
Chu vi hình bình hành ABNQ, QNDC, AMDP và BMPC là: 20 : 2 = 10cm
Tổng chu vi là: 20 + 5 x 4 + 10 x 4 = 80cm

Tham khảo
Đáp án:
Có: AMMB=ANNAAMMB=ANNA
=> MN//BC (theo đl ta-lét đảo)
Vì: MK//BI(cmt)
=> MKBI=AKAIMKBI=AKAI (theo đl ta lét) (1)
Vì: KN//IC(cmt)
=> NKIC=AKAINKIC=AKAI (thep đl ta lét) (2)
Từ (1)(2) suy ra: MKBI=NKICMKBI=NKIC
Mà BI=IC(gt)
=> MK=NK
=> K là trung điểm của MN

a: BC=1/3*6=2cm
C=(6+2)*2=8*2=16cm
b: Sửa đề: Tính diện tích hình bình hành DMBN
DM=căn 3^2+3^2=3căn 2(cm)
BM=6/2=3cm
S DMBN=3*3căn 2=9*căn 2(cm2)

a) Học sinh vẽ hình chữ nhật ABCD
b) Trên cạnh AD lấy điểm M sao cho: AM = 4 : 2 = 2 (cm)
Trên cạnh BC lấy điểm N sao cho: BN = 2cm
M và N là trung điểm của AD và BC
- Các hình chữ nhật có ở hình bên là: ABNM, MNCD, ABCD
- Các cạnh song song với cạnh AB là: MN, DC