

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



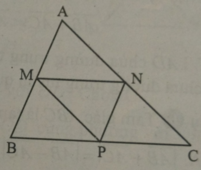
Xét tam giác ABC có M; N; P lần lượt là trung đểm của AB; AC; BC nên NP; MP là đường trung bình của tam giác.
Suy ra: NP// AB; MP// AC
Do đó, AMPN là hình bình hành.
Theo quy tắc hình bình hành ta có A M → + A N → - A P → = 0 →
Đáp án C

Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB.

Đáp án B

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm

Câu 1:
Gọi M là trung điểm của AC
AM=AC/2=2
\(BM=\sqrt{3^2+2^2}=\sqrt{13}\)
\(\left|\overrightarrow{AB}+\overrightarrow{CB}\right|=\left|\overrightarrow{BA}+\overrightarrow{BC}\right|=2\cdot BM=2\sqrt{13}\)
Câu 6:
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}+\overrightarrow{FA}\)
\(=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{EA}=\overrightarrow{AE}+\overrightarrow{EA}=\overrightarrow{0}\)

Giả sử \(B\left(x;y\right)\).Do \(M\left(2;0\right)\) là trung điểm \(BC\Rightarrow C\left(4-x;-y\right)\).
Do \(N\left(2;3\right)\) là trung điểm \(CA\) \(\Rightarrow A\left(x;6+y\right)\)
Do \(P\left(-1;3\right)\) là trung điểm \(AB\Rightarrow\left\{{}\begin{matrix}x+x=2.\left(-1\right)\\6+y+y=2.3\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2x=-2\\2y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\\ \Rightarrow B\left(-1;0\right);A\left(-1;6\right);C\left(5;0\right)\).