


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





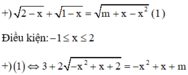
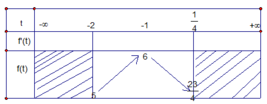
Đặt − x 2 + x = t ;
f x = − x 2 + x ; f ' x = − 2 x + 1
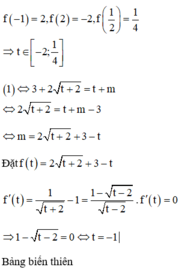

Chọn A

Chọn B.
Phương pháp:
+ Biến đổi phương trình thứ nhất của hệ để đưa về dạng
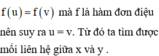
+ Thay vào phương trình thứ hai ta được phương trình ẩn y. Lập luận phương trình này có nghiệm duy nhất
thì hệ ban đầu sẽ có nghiệm duy nhất.

+ Sử dụng bất đẳng thức Cô-si để thử lại m.
Cách giải:



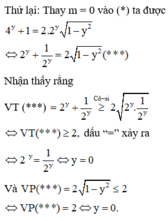
Vậy phương trình (***) có nghiệm duy nhất y = 0.
Kết luận : Với m = 0 thì hệ đã cho có nghiệm duy nhất nên tập S có một phần tử.
Chú ý :
Các em có thể làm bước thử lại như sau :
Thay m = 0 vào (*) ta được
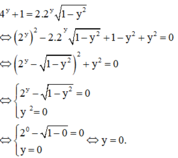

Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log x 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 x - 2 = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
m - 1 t 2 + m - 5 + m - 1 = 0 ⇔ m t 2 + t + 1 = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 t 2 - 1 t 2 + t + 1 2 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số [-1;1] đồng biến trên [-1;1]. Suy ra m i n [ - 1 ; 1 ] f ( t ) = f ( - 1 ) = - 3 m a x [ - 1 ; 1 ] f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số
f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 b , b = 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .

Đáp án B
Phương pháp:
- Biến đổi phương trình về phương trình bậc hai đối với log 2 x − 2 và đặt ẩn phụ t = log 2 x − 2 với t ∈ − 1 ; 1
- Rút m theo t và xét hàm f(t) để tìm ra điều kiện của m.
Cách giải:
m − 1 log 1 2 2 x − 2 2 + 4 m − 5 log 1 2 1 x − 2 + 4 m − 4 = 0 x > 2
m − 1 log 2 2 x − 2 + m − 5 log 2 x − 2 + m + 1 = 0
Đặt y = log 2 x − 2 ⇒ x ∈ 5 2 ; 4 ⇒ t ∈ − 1 ; 1
Phương trình đã cho trở thành:
m − 1 t 2 + m − 5 t + m + 1 = 0
⇔ m t 2 + t + 1 = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1
vì t 2 + t + 1 > 0 ∀ t ∈ − 1 ; 1
Xét hàm số: y = 1 + 4 t t 2 + t + 1 trên − 1 ; 1
Có: y ' t = − 4 t 2 + 4 t 2 + t + 1 2
y ' x = 0 ⇔ − 4 t 2 + 4 t 2 + t + 1 2 = 0 ⇔ t = ± 1 ∈ − 1 ; 1
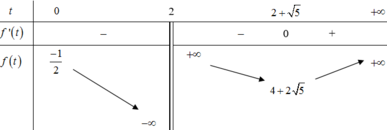
Ta có bảng biến thiên:

⇒ m ∈ − 3 ; 7 3 ⇒ a + b = − 2 3 .
Chú ý khi giải: HS thường nhầm lẫn các công thức biến đổi logarit dẫn đến kết quả sai, hoặc nhầm lẫn trong bước xét hàm f(t) để đi đến kết luận.