Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(n_{\Omega}=A_8^5-A_7^4=5880\)
Chọn 3 chữ số chẵn: \(C_4^3=4\) cách
Chọn 2 chữ số lẻ: \(C_4^2=6\) cách
Xếp 2 số lẻ liền nhau, sau đó hoán vị với 3 chữ số chẵn: \(2!.4!=48\) cách
Chọn 3 chữ số chẵn sao cho có mặt chữ số 0: \(C_3^2=3\) cách
Hoán vị 5 chữ số sao cho 2 số lẻ liền nhau và số 0 đứng đầu: \(2!.3!=12\) cách
\(\Rightarrow6.\left(4.48-3.12\right)=936\)
Xác suất: \(P=\dfrac{936}{5880}=\dfrac{39}{245}\)

Đáp án C
Xét các số có 9 chữ số khác nhau:
- Có 9 cách chọn chữ số ở vị trí đầu tiên.
- Có ![]() cách chọn 8 chữ số tiếp theo
cách chọn 8 chữ số tiếp theo
Do đó số các số có 9 chữ số khác nhau là: ![]()
Xét các số thỏa mãn đề bài:
- Có ![]() cách chọn 4 chữ số lẻ.
cách chọn 4 chữ số lẻ.
- Đầu tiên ta xếp vị trí cho chữ số 0, do chữ số 0 không thể đứng đầu và cuối nên có 7 cách xếp.
- Tiếp theo ta có ![]() cách chọn và xếp hai chữ số lẻ đứng hai bên chữ số 0.
cách chọn và xếp hai chữ số lẻ đứng hai bên chữ số 0.
- Cuối cùng ta có 6! cách xếp 6 chữ số còn lại vào 6 vị trí còn lại.
Gọi A là biến cố đã cho, khi đó
![]()
Vậy xác suất cần tìm là ![]()

Gọi số có 5 chữ số dạng \(\overline{abcde}\)
a có 9 cách chọn, b có 9 cách, c có 8 cách, d có 7 cách, e có 6 cách
\(\Rightarrow n\left(\Omega\right)=9.9.8.7.6=27216\)
- Nếu de cùng lẻ: chọn de từ 5 chữ số lẻ và xếp thứ tự: \(A_5^2=20\) cách
a có 7 cách chọn, b có 7, c có 6 cách \(\Rightarrow20.7.7.6=5880\) số
- Nếu de cùng chẵn:
+ de có chứa số 0: có \(1.4.2!.A_8^3=2688\) cách
+ de không chứa số 0: có \(A_4^2.7.7.6=3528\)
Tổng cộng: \(5880+2688+3528=12096\) số
Xác suất: \(P=\dfrac{12096}{27216}=\dfrac{4}{9}\)

Không gian mẫu: \(A_9^5\)
Gọi số cần lập có dạng \(\overline{abcde}\)
\(\Rightarrow e\) có 4 cách chọn
Chọn bộ abcd:
- Chọn 2 số lẻ từ 5 số lẻ và hoán vị chúng: \(A_5^2\) cách
- Chọn 2 số chẵn từ 3 số chẵn còn lại (khác e): \(C_3^2\) cách
\(\Rightarrow\) Bộ abcd có \(A_5^2.C_3^2.3!\) cách
Xác suất: \(P=\dfrac{4.A_5^2.C_3^2.3!}{A_9^4}=...\)




Chọn D
Số phần tử của không gian mẫu là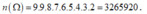
Gọi số cần tìm là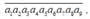
* Trường hợp a 2 = 0: Khi đó a 1 , a 3 lẻ nên có A 5 2 cách xếp, hai chữ số lẻ còn lại có C 3 2 A 6 2 cách xếp, 4 chữ số chẵn còn lại có 4! cách xếp. Vậy theo quy tắc nhân có
A 5 2 C 3 2 A 6 2 .4! = 43200 (số)
Vậy xác suất cần tính là: