
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b:
Ta có: MN\(\perp\)AC
AB\(\perp\)AC
Do đó: MN//AB
Xét ΔACB có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
=>\(\dfrac{AN}{AC}=\dfrac{1}{2}\)
c:
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
=>MA=MB
=>ΔMAB cân tại M
Ta có: \(\widehat{DAB}+\widehat{MAB}=\widehat{MAD}=90^0\)
\(\widehat{HAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
mà \(\widehat{MAB}=\widehat{HBA}\)(ΔMAB cân tại M)
nên \(\widehat{DAB}=\widehat{HAB}\)
=>AB là tia phân giác của góc DAH

Bài 6:
a: Xét ΔAPC có
M là trung điểm của AC
Q là trung điểm của PC
Do đó: MQ là đường trung bình của ΔAPC
Suy ra: MQ//AP
Xét ΔBMQ có
P là trung điểm của BQ
PD//MQ
Do đó: D là trung điểm của BM
Suy ra: DB=DM

Sửa đề: \(\left(4-\dfrac{u}{2}\right)\left(\dfrac{u^2}{4}+2u+16\right)=4^3-\left(\dfrac{u}{2}\right)^3=64-\dfrac{u^3}{8}\)

a: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
b: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
BH=6^2/10=3,6cm
CH=10-3,6=6,4cm
c: AM=BC/2=5cm
=>HM=1,4cm
S HAM=1/2*1,4*4,8=3,36cm2

a) Áp dụng định lí Pytago vào ΔABC vuông tại A,ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm

a: Xét ΔCAE có
CD là đường cao
CD là trung tuyến
CD=AE/2
Do đó:ΔCAE vuông cân tại C
b: Xét ΔHAB có HI/HA=HK/HE
nên IK//AE và IK=1/2AE
=>IK=AD=BC
Xét tứ giác BIKC có
IK//BC
IK=BC
Do đó: BIKC là hình bình hành

a) Xét ΔHBAΔHBAvà ΔHACΔHAC có:
ˆAHB=ˆCHA=900AHB^=CHA^=900
ˆHBA=ˆHACHBA^=HAC^ cùng phụ với góc BAH
suy ra: ΔHBA ΔHACΔHBA ΔHAC
P/S: câu b áp dụng hệ thức lượng. ra số hơi xấu nhé
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)

a: Mình chỉ nêu ra thôi, chứng minh thì chắc chắn đều theo trường hợp g-g nha bạn
ΔADH đồng dạng vơi ΔAFB
ΔAEH đồng dạng với ΔAFC
ΔBFH đồg dạng với ΔBEC
ΔAFB đồng dạng vơi ΔBDC
ΔBEC đồng dạng với ΔAFC
ΔBAE đồng dạng với ΔCAD
ΔAHD đồng dạng với ΔCHF
ΔCHE đồng dạng với ΔBHD
ΔAHE đồng dạng vơi ΔBHF
ΔADE đồng dạng với ΔACB
ΔBDF đồng dạng với ΔBCA
ΔCFE đồng dạng với ΔCAB


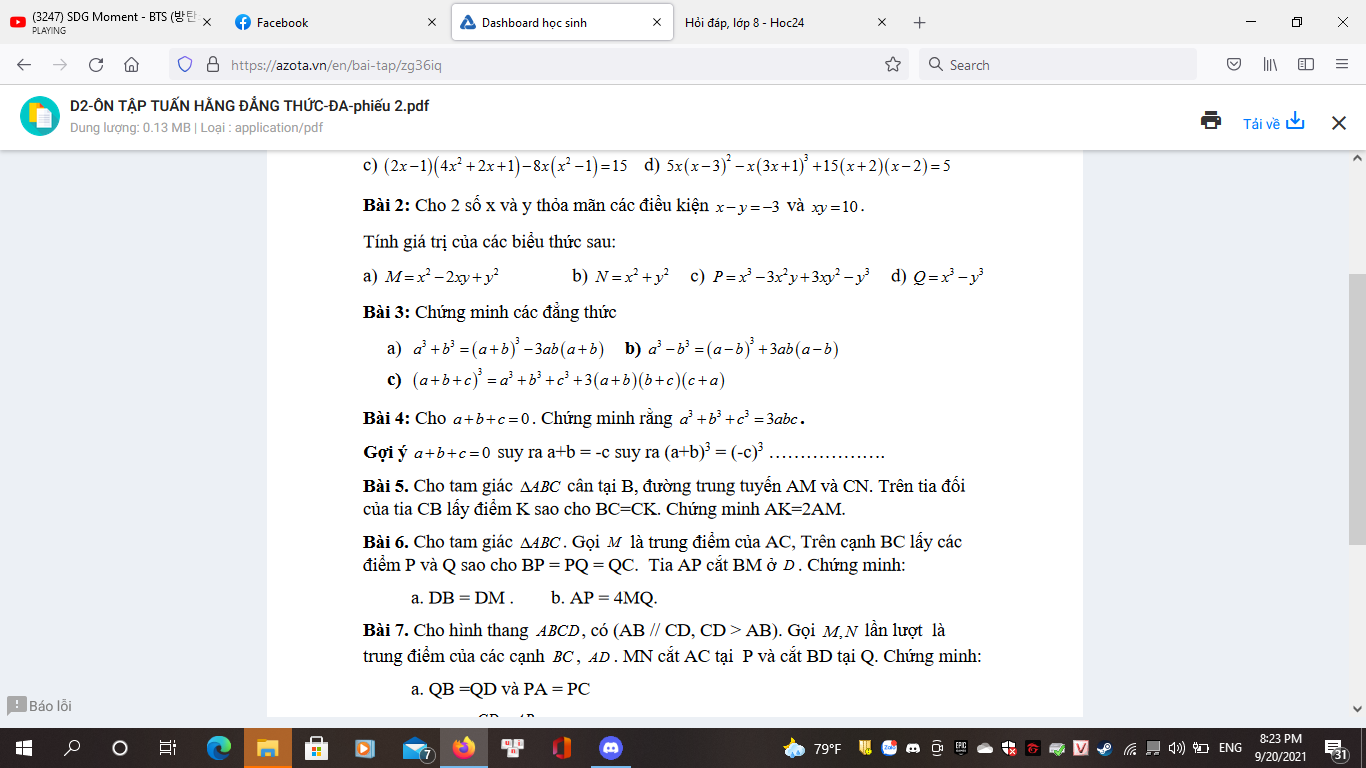 mng giúp mình bài 2 bài 3 bài 4 vs ah
mng giúp mình bài 2 bài 3 bài 4 vs ah