Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x và y lần lượt là giá tiền mỗi quả quýt và mỗi quả cam. (x > 0; y > 0)
Vân mua 10 quả quýt, 7 quả cam hết 17800 đồng nên ta có:
10x + 7y = 17800
Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng nên ta có:
12x + 6y = 18000
Từ đó ta có hệ:
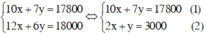
Từ (2) rút ra được y = 3000 – 2x, thay vào (1) ta được :
10x + 7.(3000 – 2x) = 17800
⇔ 10x + 21000 – 14x = 17800
⇔ 4x = 3200 ⇔ x = 800 (thỏa mãn)
Thay x = 800 vào y = 3000 – 2x ta được y = 1400 (thỏa mãn)
Vậy giá tiền một quả quýt là 800đ và giá tiền một quả cam là 1400đ.

Gọi x là số kg cam
y là số kg quýt
Theo đề , ta có
\(\hept{\begin{cases}x+y=6\\15000x+20000y=100000\end{cases}}\)
\(\hept{\begin{cases}x=4\\y=2\end{cases}}\)

Giải:
2/3 cây cam = 3/5 cây quýt và = 6/7 cây vải thều hay 6/9 cây cam = 6/10 cây quýt = 6/7 cây vải thều
Vậy số cây cam chiếm 9 phần, số cây quýt chiếm 10 phần và số cây vải thều chiếm 7 phần.
Số cây cam là: 1950 : ( 9 + 10 + 7 ) * 9 = 675 ( cây )
Số cây quýt là: 1950 : (9 + 10 + 7 ) * 10= 750 (cây)
Số cây vải thều là: 1950 - ( 675 + 750 ) = 525 (cây)
Đ/S: Cam : 675 cây ; quýt : 750 cây ; vải thều : 525 cây .
![]()

Gọi số quýt ban đầu ở mỗi rổ là x (quả)
Muốn lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở mỗi rổ lúc đầu phải nhiều hơn 30 quả hay x > 30.
Khi đó rổ thứ nhất còn x – 30 quả; rổ thứ hai có x + 30 quả.
Vì số quả ở rổ thứ hai bằng 1/3 bình phương số quả còn lại ở rổ thứ nhất nên ta có phương trình:
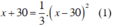
Giải phương trình (1):
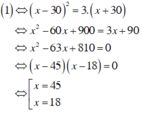
Vì x > 30 nên x = 45 thỏa mãn.
Vậy ban đầu mỗi rổ có 45 quả cam.

Sau khi mua thì Cường còn lại \(\frac{3}{5}=\frac{15}{25}\) số tiền, Huy còn lại \(\frac{5}{7}=\frac{15}{21}\) số tiền.
Ta thấy thấy tiền của Cường có 25 phần thì tiền của Huy có 21 phần.
Giá trị 1 phần là:
219000:(15+15)=7300 (đồng)
Tiền của Cường có được là:
7300x25=182500(đồng)
Tiền của Huy có được là:
7300x21=153300 (đồng)
Đáp số:153300 đồng

Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình:
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được:
3 x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7 x + 4 y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được:
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
\(10x+7y=17800\)
\(12x+6y=18000\)
<=> Hệ phương trình \(10x+7y=17800\)
\(2x+y=3000\)
<=> Hệ phương trình 2x + y = 3000
2y = 28000
<=> x= 800 và y = 1400.
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đông
Vân:10 quả quýt,7 quả cam=17 800 đồng
Lan:12 quả quýt,6 quả cam=18 000 đồng
Nếu cả số quýt và cam của vân mua gấp lên 2 lần thì đc
20 quýt+14 cam=35 600 đồng
-12 quýt+6 cam=18 000đông
=8 quýt+8 cam=17 600 đồng
giá tiền 1 quả quýt là: 17 600 -8=17 592 đồng
giá tiền1 quả cam là: 17 6 00- 17 592 =8