Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng công thức tính chu kì của con lắc đơn dao động điều hoà
Cách giải:
Ta có:
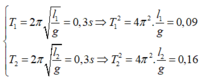
Chu kỳ của con lắc có chiều dài: l3 = l1 + l2 và
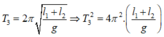
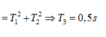

Ta có: \(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow l=\dfrac{T\sqrt{g}}{2\pi}\)
Theo đề: \(\left\{{}\begin{matrix}l_3=l_1+l_2\\l_4=l_1-l_2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}l_1=\dfrac{l_3+l_4}{2}\\l_2=\dfrac{l_3-l_4}{2}\end{matrix}\right.\)
Ta có: \(l_1=\dfrac{\sqrt{g}\left(T_3+T_4\right)}{4\pi}=0,8\)
\(l_2=\dfrac{g\left(T_3^2-T_4^2\right)}{8\pi^2}=0,64\)

\(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow T^2\) tỉ lệ thuận với l
Theo bài ra
\(\left\{{}\begin{matrix}T_1^2+T_2^2=\left(2,7\right)^2=7,29\\T_1^2-T_2^2=\left(0,9\right)^2=0,81\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}T_1^2=4,05\\T_2^2=3,24\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}T_1=2,01s\\T_2=1,8s\end{matrix}\right.\)

\(T_1=2\pi\sqrt{\dfrac{l_1}{g}}\left(1\right),T_2=2\pi\sqrt{\dfrac{l_2}{g}}\left(2\right)\)
\(T=2\pi\sqrt{\dfrac{l_1-l_2}{g}}\left(3\right)\)
Thay (1),(2) vào (3) ta được:
\(T=\sqrt{T_1^2-T_2^2}=1.5s\) ->C

Đáp án C
Khi con lắc đơn có chiểu dài l 1 : T 1 2 = 4 π 2 l 1 g
Khi con lắc đơn có chiều dài l 2 : T 2 2 = 4 π 2 l 2 g
Khi con lắc đơn có chiều dài: l 2 - l 1
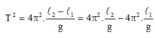
![]()
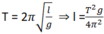
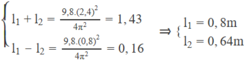
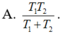
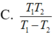
Chọn B