Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
- Giả sử M gần A hơn so với B, N gần B hơn so với A
M thuộc dãy cực đại bậc 3 ⇒ M A − M B = − 3 λ
N thuộc dãy cực tiểu thứ 4 ⇒ N A − N B = 3 , 5 λ
- Ban đầu số điểm dao động với biên độ cực đại trên MN là nghiệm của bất phương trình: M A − M B ≤ k 3 λ ≤ N A − N B ⇔ − 3 ≤ k ≤ 3 , 5
Vậy có 7 điểm dao động với biên độ cực đại trên MN
- Tăng tần số lên 3,5 lần thì bước sóng giảm đi 3,5 lần ⇒ λ ' = λ / 3 , 5
- Số điểm dao động với biên độ cực đại trên MN lúc sau là M A − M B ≤ 3 λ ' ≤ N A − N B ⇔ − 3 λ ≤ k λ 3 , 5 ≤ 3 , 5 λ ⇔ − 10 ≤ k ≤ 12
Vậy có 23 điểm dao động với biên độ cực đại trên MN, tức là so với ban đầu đã tăng 16 điểm

Đáp án D
Sóng tại M có biên độ triệt tiêu nên M là cực tiểu
![]()
Giữa M và đường trung trực AB có 5 đường cực đại nên M là cực tiểu có k = 5

Đáp án B
Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d 2 và d 1
Ta có AD − BD ≤ d 2 − d 1 ≤ AC − BC
+ Điểm cực đại trên đoạn CD thỏa mãn: d 2 − d 1 = kλ, k = 0, ± 1, ± 2, ± 3 ... với ⇒ AD − BD ≤ kλ ≤ AC − BC ⇔ AD − BD λ ≤ k ≤ AC − BC λ
⇒ − 3 , 3 ≤ k ≤ 3 , 3
Có 7 giá trị của k là 0, ± 1, ± 2, ± 3 nên có 7 điểm cực đại trên CD
+ Điểm cực tiểu trên đoạn CD thỏa mãn: d 2 − d 1 = 2 k + 1 λ 2 , với k = 0, ± 1, ± 2, ± 3 ...
⇒ AD − BD ≤ 2 k + 1 λ 2 ≤ AC − BC ⇔ 2 AD − BD λ ≤ 2k + 1 ≤ 2 AC − BC λ ⇒ − 3 , 8 ≤ k ≤ − 2 , 83
Có 6 giá trị của k thỏa mãn k = 0, ± 1, ± 2, − 3 , − 2 nên có 6 điểm cực tiểu trên CD




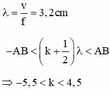
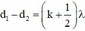
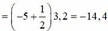


Đáp án D
Khoảng cách giữa hai điểm cực tiểu liên tiếp trên đoạn thẳng nối hai nguồn là