Hai phương trình không tương đương.

Giải pt \(\dfrac{x}{3}+1=0\)

\(\Leftrightarrow\dfrac{x}{3}=-1\Leftrightarrow x=-1.3\Leftrightarrow x=-3\)

Vậy 2 pt đó tương đương nhau

`x/3 +1 = 0`

`<=> x/3 = -1`

`<=> x=-3.`

Vậy `2` phương trình tương đương với nhau

1:

a: x^3+x^2-3x-3=0

=>x^2(x+1)-3(x+1)=0

=>(x+1)(x^2-3)=0

=>x=-1 hoặc x^2-3=0

=>\(S_1=\left\{-1;\sqrt{3};-\sqrt{3}\right\}\)

2x+3=1

=>2x=-2

=>x=-1

=>S2={-1}

=>Hai phương trình này không tương đương.

1: \(\dfrac{1}{\left|x+1\right|}+\dfrac{1}{x+2}=3\left(1\right)\)

TH1: x>-1

Pt sẽ là \(\dfrac{1}{x+1}+\dfrac{1}{x+2}=3\)

=>\(\dfrac{x+2+x+1}{\left(x+1\right)\left(x+2\right)}=3\)

=>3(x+1)(x+2)=2x+3

=>3x^2+9x+6-2x-3=0

=>3x^2+7x+3=0

=>\(\left[{}\begin{matrix}x=\dfrac{-7-\sqrt{13}}{6}\left(loại\right)\\x=\dfrac{-7+\sqrt{13}}{6}\left(nhận\right)\end{matrix}\right.\)

TH2: x<-1

Pt sẽ là:

\(\dfrac{-1}{x+1}+\dfrac{1}{x+2}=3\)

=>\(\dfrac{-x-2+x+1}{\left(x+1\right)\left(x+2\right)}=3\)

=>\(\dfrac{-1}{\left(x+1\right)\left(x+2\right)}=3\)

=>-1=3(x+1)(x+2)

=>3(x^2+3x+2)=-1

=>3x^2+9x+6+1=0

=>3x^2+9x+7=0

Δ=9^2-4*3*7

=81-84=-3<0

=>Phương trình vô nghiệm

Vậy: \(S_3=\left\{\dfrac{-7+\sqrt{13}}{6}\right\}\)

x^2+x=0

=>x(x+1)=0

=>x=0 hoặc x=-1

=>S4={0;-1}

=>S4<>S3

=>Hai phương trình này không tương đương

- Phương trình x = 0 có tập nghiệm S1 = {0}.

- Xét phương trình x(x - 1) = 0. Vì một tích bằng 0 khi một trong hai thừa số bằng 0 tức là:

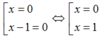
Nên phương trình này có tập nghiệm S2 = {0; 1}.

Vì S1 ≠ S2 nên hai phương trình không tương đương.

co vi co cug 1 tap nghiiem

a) Tương đương             b) Không tương đương