Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
b)Nếu tăng khoảng cách lên 2 lần thì \(F_{hd}\) giảm 4 lần.
Khi đó: \(F'_{hd}=\dfrac{2,1\cdot10^{-6}}{4}=5,25\cdot10^{-7}N\)
c)Để lực hấp dẫn giữa hai quả cầu lớn nhất thì khoảng cách giữa chúng phải nhỏ nhất.
\(F_{max}=\dfrac{G\cdot m_1m_2}{\left(2R\right)^2}\)

\(R=\sqrt{\dfrac{mM\cdot G}{F_{hd}}}=\sqrt{\dfrac{50\cdot50\cdot6,67\cdot10^{-11}}{26,68\cdot10^{-7}}}=0,25\left(m\right)\)

Đáp án D

Để lực hấp dẫn lớn nhất thì khoảng cách giữa hai quả nhỏ nhất
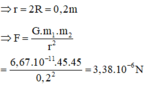

\(F_{hapdan}=G\dfrac{m'm''}{r^2}=6,67\cdot10^{-11}\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,8\cdot10^5\cdot1000\right)^2}=.......\left(N\right)\)
\(F=G\cdot\dfrac{M_1M_2}{d^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,8\cdot10^5\cdot10^3\right)^2}=2\cdot10^{20}\)(N)
Chọn C

\(F_{hd}=G.\dfrac{m_1m_2}{r^2}=6,67.10^{-11}.\dfrac{\left(3.10^5\right)^2}{50^2}=...\left(N\right)\)

Chọn đáp án A
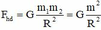
+ Ta thấy: G và m không đổi suy ra: ![]() =0,1m
=0,1m
Vậy khi F h d m a x thì hai quả cầu đặt sát nhau
+ Suy ra 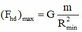
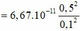
![]()
Lực hấp dẫn của hai quả cầu:
\(F_{hd}=G\cdot\dfrac{m_1m_2}{r^2}\)
\(=6,67\cdot10^{-11}\cdot\dfrac{500\cdot250}{2^2}=2,1\cdot10^{-6}N\)
vậy 2 bán kính của 2 quả cầu ko cần + vô đúng ko bạn