Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để hàm số đồng biến thì a>0 => m-1>0 <=> m>1
b) Thay M(2;1) vào h/s
1=(m-1).2+2m-5 => m=2
c) Để d song song với đường thẳng trên thì a=a' \(m-1=3\Leftrightarrow m=4\)
d) Cắt 1 điểm trên trục tung thì b=b' \(\Leftrightarrow2m-5=3\Leftrightarrow m=4\)

a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)

1: Khi m=3/2 thì \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x+3=2x+3\)
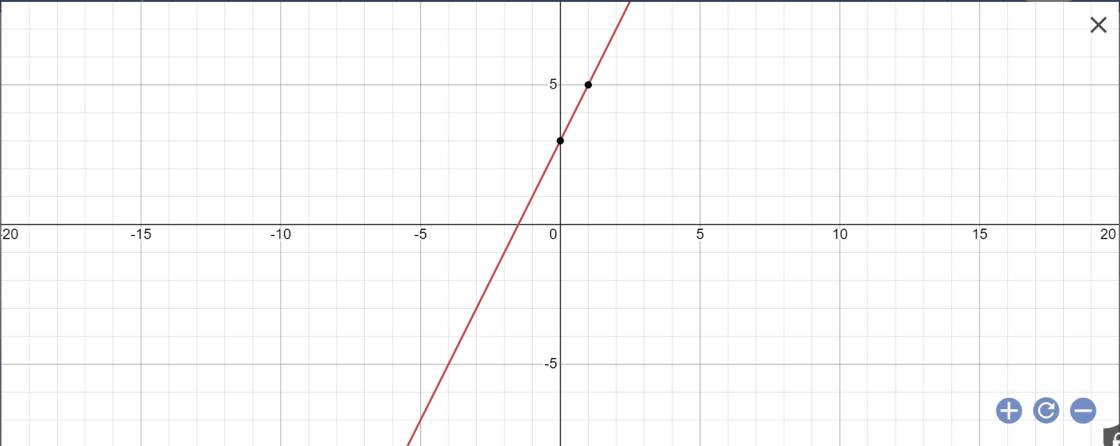
2: \(tanx=a=2m-1\)
3:
Để hai đồ thị (d) và (d') song song với nhau thì:
\(2m-1=3\)
=>2m=4
=>m=2
4: Thay x=1 vào (d1), ta được:
\(y=2\cdot1-3=-1\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(2m-1\right)+3=-1\)
=>2m+2=-1
=>2m=-3
=>\(m=-\dfrac{3}{2}\)
5: y=1
=>2x-3=1
=>2x=4
=>x=2
Thay x=2 và y=1 vào (d),ta được:
\(2\left(2m-1\right)+3=1\)
=>2(2m-1)=-2
=>2m-1=-1
=>2m=0
=>m=0

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)

a: Để hàm số đồng biến thì 1-m>0
hay m<1
b: Thay x=2 và y=-1 vào (d), ta được:
2-2m+m-1=-1
=>-m+1=-1
=>-m=-2
hay m=2

Đáp án C
• Ta thấy d: y = (m + 2)x - m có a = m + 2 và d': y = -2x - 2m + 1 có a' = -2
• Để y = (m + 2)x - m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ -2
• Để d cắt d' ⇔ a ≠ a' ⇔ m + 2 ≠ -2 ⇔ m ≠ -4
Vậy m ≠ -2; m ≠ -4

+) Ta thấy d : y = ( m + 2 ) x – m c ó a = m + 2 v à d ’ : y = − 2 x − 2 m + 1 c ó a ’ = − 2
+) Để y = ( m + 2 ) x – m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ − 2 .
+) Để d cắt d’ ⇔ a ≠ a ’
m + 2 ≠ − 2 ⇔ m ≠ − 4 V ậ y m { − 2 ; − 4 }
Đáp án cần chọn là: C
a:
Sửa đề: d: y=(m+2)x-m; d': y=-2x-2m+1
Để d và d' cắt nhau thì \(m+2\ne-2\)
=>\(m\ne-4\)